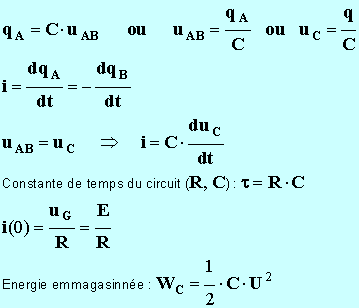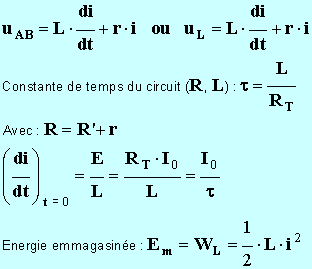|
|
|
Définition : Une onde mécanique correspond à la propagation d’une perturbation dans un milieu matériel sans transport de matière. - Onde longitudinale : - La direction de déplacement temporaire de la matière et la direction de propagation de l'onde sont les mêmes. - On parle aussi d'ondes de compression : - elles créent de proche en proche des ondes de compression -détente du milieu de propagation. - Elles vibrent parallèlement à leur direction de propagation (cas du ressort) - Onde transversale : - la direction de déplacement temporaire de la matière et la direction de propagation de l'onde sont perpendiculaires. - On parle aussi d'ondes de cisaillement. - Elles vibrent perpendiculairement à leur direction de propagation (cas de la corde) |
La vitesse à laquelle la perturbation se propage s’appelle la célérité de l’onde (Référentiel)
- La célérité est le quotient de la distance parcourue sur la durée de parcours.
-

Influence de l’inertie du milieu.
- L’inertie d’un milieu ou d’un système représente la résistance que ce milieu ou ce système oppose lorsqu’on cherche à le mettre en mouvement.
- La célérité d’une onde dans un milieu dépend de son inertie.
- Plus l’inertie du milieu est grande et plus la célérité de l’onde se propageant dans ce milieu est faible.
Influence de la rigidité d’un milieu.
- La rigidité d’un milieu représente la résistance que ce milieu oppose lorsqu’on cherche à le déformer.
- La célérité d’une onde dépend de la rigidité du milieu dans lequel elle se propage.
- Plus le milieu est rigide et plus grande est sa célérité.
La perturbation crée au point S de la corde au temps t0 se propage de proche en proche.
Elle atteint le point M, puis le point M’ du milieu matériel.
Chaque point du milieu matériel reproduit la perturbation de la source S (on suppose que la perturbation se propage sans amortissement).
- La perturbation au point M reproduit la perturbation de la source S avec un retard t, car la perturbation met un certain temps pour progresser de S à M.
- Le retard t est la durée mise par l’onde pour se propager de S à M :
2.
Les ondes progressives périodiques.
![]()
L’onde progressive possède une périodicité temporelle (période T de la source)
L’onde progressive possède une périodicité spatiale (la longueur d’onde l en m)
|
- Définition : - La longueur d’onde λ est la distance séparant deux points consécutifs du milieu qui vibrent en phase. - Définition : - La longueur d’onde λ est la distance parcourue par l’onde en une période T. |
- Si d est la distance qui sépare deux points qui vibrent en phase alors : d = k . λ avec k Î N *
-
Relation fondamentale :

Dispersion et diffraction des ondes.
- Un milieu est dispersif si la célérité de l’onde dans le milieu dépend de la fréquence imposée par la source.
- Le phénomène de diffraction dépend des dimensions de l’ouverture ou de l’obstacle.
- Ce phénomène se manifeste si les dimensions de l’ouverture ou d’un obstacle sont du même ordre de grandeur que la longueur d’onde.
- L’onde diffractée a même fréquence et même longueur d’onde que l’onde incidente.
3.
Modèle ondulatoire de la lumière.
![]()
L’onde lumineuse résulte de la propagation d’une perturbation électromagnétique dans les milieux transparents.
Les ondes lumineuses périodiques sont appelées des radiations.
- La célérité de la lumière dans le vide est une constante universelle de valeur approchée : c ≈ 3,00 x 10 8 m / s
- Une radiation lumineuse est caractérisée par :
- Sa fréquence n (en Hz) ou sa période T (en s).
-
Sa longueur d’onde dans le vide
λ 0 :

- Le domaine de radiations lumineuses visibles s’étend de 400 nm (violet) à 800 nm (rouge).
Étude quantitative de la diffraction de la lumière.
|
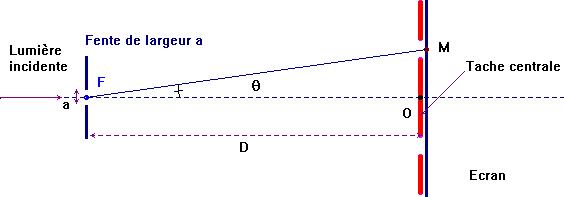
- Définition de l’écart angulaire θ. - L’écart angulaire est l’angle sous lequel est vue la moitié de la tache centrale depuis l’objet diffractant. - C’est le demi-diamètre angulaire de la tache centrale. |
- Schéma :
-
 et
et
![]()
Dispersion de la lumière.
- Le verre est un milieu dispersif. Il faut préciser la valeur de l’indice pour chaque radiation.
4.
![]()
- L’unité de masse atomique u est le douzième de la masse du carbone 12.
- 1 u = 1,6605402 x 10 – 27 kg.
Les Émissions Radioactives.
- Une source radioactive peut émettre : Des particules et Un rayonnement g.
- Les particules émises sont de trois types : les particules α, β + et β -.
Définition.
-
Lorsqu’un noyau
![]() est instable, il subit une transformation
spontanée conduisant à la formation d’un nouveau noyau
est instable, il subit une transformation
spontanée conduisant à la formation d’un nouveau noyau ![]() .
.
-
Ce phénomène porte le nom de radioactivité.
![]() est appelé le noyau père et
est appelé le noyau père et ![]() est appelé le noyau fils.
est appelé le noyau fils.
Les Lois de conservation : Loi de Soddy.
- Toutes les réactions nucléaires vérifient les lois de conservation suivantes :
- Conservation de la charge électrique (conservation du nombre de charge total)
- Conservation du nombre total de nucléons.
|
- Lois de Soddy : - Conservation du nombre de nucléons : A = A' + a - Conservation de la charge globale : Z = Z' + z |
||||||||||||||||
Radioactivité α.
- Un noyau lourd instable éjecte une particule α et donne un noyau fils plus léger, généralement dans un état excité
|
A Z |
X |
¾® |
A' Z' |
Y |
+ |
4 2 |
He |
| Noyau-père | Noyau-fils | Particule α | |||||
|
- Conservation du nombre de nucléons : |
A' = A - 4 |
|
- Conservation de la charge globale : |
Z' = Z - 2 |
Radioactivité β -.
- Cette radioactivité se manifeste lorsque le noyau présente un excès de neutrons.
-
Au cours de la désintégration, il y a émission d’un électron
noté
![]() .
.
|
A Z |
X |
¾® |
A Z + 1 |
Y |
+ |
0 - 1 |
e |
| Noyau-père | Noyau-fils | Particule β - | |||||
|
- Conservation du nombre de nucléons : |
A' = A |
|
- Conservation de la charge globale : |
Z' = Z + 1 |
La radioactivité β +.
- Cette radioactivité se manifeste lorsque le noyau d’un atome possède trop de protons.
-
Au cours de la désintégration, il y a émission d’un positon
noté ![]() .
.
|
A Z |
X |
¾® |
A Z - 1 |
Y |
+ |
0 + 1 |
e |
| Noyau-père | Noyau-fils | Particule β + | |||||
|
- Conservation du nombre de nucléons : |
A' = A |
|
- Conservation de la charge globale : |
Z' = Z - 1 |
La désexcitation γ.
- Le noyau-fils est le plus souvent dans un état instable, il libère son excédant d’énergie sous forme de rayonnement γ.
- Il se désexcite.
|
A Z |
Y |
¾® |
A' Z' |
Y* |
+ |
0 0 |
γ |
| Noyau-fils
Etat excité |
Noyau-fils
Etat stable |
Rayonnement | |||||
Loi de décroissance radioactive.
|
- énoncé : Loi de décroissance radioactive. - Le nombre de noyaux radioactifs N (t) présents à la date t dans un échantillon est donné par la loi de décroissance radioactive - N (t) = N0 e - λ t - N0 représente le nombre de noyaux radioactifs initialement présents. |
Demi-vie t1/2.
|
- Définition : Pour un type de noyaux radioactifs, la demi-vie t1/2 est la durée au bout de laquelle la moitié des noyaux radioactifs initialement présent dans l’échantillon se sont désintégrés. |
-
Relation entre t1/2
et
λ :

Courbe de décroissance et Constante de temps τ : τ = 1 / λ

Activité d’un échantillon radioactif.
- L’activité A(t) d’un échantillon radioactif à la date t est le nombre de désintégrations par seconde de cet échantillon.
- L’unité d’activité est le Becquerel Bq en hommage à Henri Becquerel.
- 1 Bq = 1 désintégration par seconde.
- A (t) = A 0 e - λ t
La datation au carbone 14.
- Elle
est fondée sur l’utilisation de la loi de décroissance radioactive de l’isotope
![]() , radioactif
β -.
, radioactif
β -.
- La demi-vie du carbone 14 est fixée de façon conventionnelle à
- t 1/2 = 5568 ± 30 ans (valeur admise en 1950).
- Le carbone 14 est présent dans l’atmosphère.
- Il est régénéré par une réaction nucléaire faisant intervenir des neutrons cosmiques et des noyaux d’azote 14 :
|
14 7 |
N |
+ |
1 0 |
n |
¾® |
14 6 |
C |
+ |
1 1 |
H |
5.
Masse et énergie : réactions nucléaires.
![]()
Énergie de masse.
- Dans la théorie de la relativité restreinte, en 1905, Einstein a montré que la masse est une forme d’énergie.
- Toute particule de masse m, au repos, possède une énergie :
|
E = m . c 2 |
E énergie en joule (J) |
|
m masse en kilogramme (kg) |
|
|
c célérité de la lumière dans le vide (m / s) |
-
Pour les calculs, on prend la valeur approchée : c
= 3,00
× 10
une autre unité d’énergie.
| 1 eV = 1,6 × 10 –19 J | 1 MeV = 1,6 × 10 –13 J |
Défaut de masse d’un noyau.
- La masse d’un noyau atomique au repos est toujours inférieure à la somme des masses des nucléons qui le constituent.
- Les nucléons étant pris séparément et au repos.
-
Le noyau de symbole
:
![]() est constitué de Z
protons et de ( A – Z ) neutrons
est constitué de Z
protons et de ( A – Z ) neutrons
- La masse des nucléons : Z . m p + (A – Z) . m n.
- La masse du noyau X est m noyau alors : m X = m noyau < Z . m p + (A – Z) . m n
- La quantité : [Z . m p + (A – Z) . m n] - m X représente le défaut de masse du noyau.
- C’est une grandeur strictement positive.
Une autre unité de masse.
- Les physiciens préfèrent utiliser le MeV / c 2 comme unité de masse.
- Cette unité découle de la relation :
-

Énergie de liaison d’un noyau.
-
L’énergie de liaison E
l d’un
noyau
![]() est l’énergie libérée lors de la formation du noyau à partir des nucléons au
repos.
est l’énergie libérée lors de la formation du noyau à partir des nucléons au
repos.
- Puisque la masse du système diminue, le système libère de l’énergie.
- C’est cette énergie que l’on appelle l’énergie de liaison.
- E l = | Δm | . c 2 Avec : | Δm | = | [m X – Z . m p + (A – Z) . m n] |
|
Z . |
1 1 |
H |
+ (A - Z) . |
1 0 |
n |
¾® |
A Z |
X |
L ‘énergie de liaison par nucléon.
- La connaissance de l’énergie de liaison par nucléon est très utile car elle permet de comparer la stabilité des différents noyaux.
- L’énergie de liaison par nucléon est donnée par la relation :
-
 C’est le quotient de l’énergie
de liaison par le nombre de nucléon du noyau.
C’est le quotient de l’énergie
de liaison par le nombre de nucléon du noyau.
Stabilité des noyaux et Courbe d’Aston.
La réaction de fission
- La réaction de fission est une réaction nucléaire provoquée.
- Au cours d’une fission nucléaire, un neutron lent (neutron thermique) brise un noyau lourd fissile en deux noyaux légers.
- Cette réaction libère de l’énergie.
- Équation-bilan :
|
1 0 |
n |
+ |
235 92 |
U |
¾® |
236 92 |
U |
¾® |
A1 Z1 |
X1 |
+ |
|
A2 Z2 |
X2 |
+ |
|
k . |
1 0 |
n |
+ |
g |
| Neutron | Uranium 235 | noyau
fissile |
Neutron | ||||||||||||||||||
La fusion nucléaire.
- Au cours d’une fusion nucléaire, deux noyaux légers s’unissent pour former un noyau lourd.
- C’est une réaction nucléaire provoquée qui libère de l’énergie.
- Exemple : fusion d’un noyau de deutérium et d’un noyau de tritium.
|
2 1 |
H |
+ |
3 1 |
H |
¾® |
4 2 |
He |
+ |
1 0 |
n |
| Deutérium | Tritium | Particule a | Neutron | |||||||
Bilan énergétique d’une réaction nucléaire.
- Une réaction nucléaire s’accompagne toujours d’une diminution de la masse du système : Dm = m f – m i < 0
- Au cours de la réaction, le système cède de l’énergie au milieu extérieur.
- L’énergie libérée par le système a pour expression :
|
Elib = | m f – m i | . c 2 Elib = | Δ m | . c 2 |
Elib énergie en joule (J) |
|
| mf – mi | perte de masse en kilogramme (kg) |
|
|
c célérité de la lumière dans le vide (m / s) |
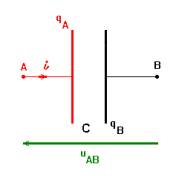
Les condensateurs.
- Un condensateur est formé de deux conducteurs métalliques appelés armatures, séparés par un isolant qui peut être de l'air ou un diélectrique.

Capacité d’un condensateur :
- Un condensateur est caractérisé par une grandeur physique appelée capacité, notée C (farad F)
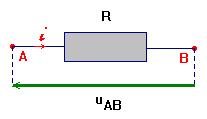
- Représentation : convention récepteur :

-
 ou
qA
= C . uAB
et
ou
qA
= C . uAB
et

Charge à intensité constante. (TP Physique N° 06)

Charge d’un condensateur par un échelon de tension. (TP Physique N° 07)

- On appelle constante de temps du circuit (R, C), la valeur : τ = R.C (seconde s)
- Remarque :
|
Si on charge le condensateur pendant la durée Δt = τ , la charge Qτ portée par le condensateur est égale à 63 % de sa charge maximale Qmax. |
- Équation différentielle :
- Loi d’ohm aux bornes du conducteur ohmique : u DA = R . i
-
Loi d’ohm aux bornes
du condensateur :

-
Relation entre l’intensité et la tension u
AB :

- Loi d’additivité des tensions :
-

- On reconnaît une équation différentielle du premier ordre avec deuxième membre qui admet une solution du type :
- uAB (t) = A e k t + B où A, B et k sont des constantes.
-
Solution :

- Remarque : si on charge le condensateur pendant la durée Δt = τ , la tension aux bornes du condensateur est égale à 63 % de la tension E.

Énergie emmagasinée dans un condensateur.
- Expression de l'énergie.
- Un condensateur de capacité C chargée sous la tension u emmagasine l’énergie :

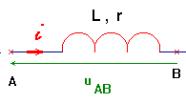
Caractéristiques d’une bobine.
- Représentation symbolique d’une bobine.
- Une bobine est un dipôle, de bornes A et B, caractérisé par son inductance L exprimée en henry (symbole H).
- L'inductance L de la bobine est une constante positive qui ne dépend que des caractéristiques.
- Une bobine est aussi caractérisée par sa résistance r qui s’exprime en ohm (Ω).
-
 Une
bobine est caractérisée par son inductance L
et sa résistance r.
Une
bobine est caractérisée par son inductance L
et sa résistance r.
- expression de la tension aux bornes d’une bobine.
- La bobine étant orientée de A vers B, la tension uAB aux bornes de la bobine est donnée par la relation :
-

| Tension aux bornes d’une bobine : uAB tension en volt (V) | ||||||||
|
+ |
r . i |
{ |
I intensité en ampère (A) |
||||
|
r résistance en ohm (Ω) |
||||||||
|
L inductance en henry (H) |
||||||||
|
|
||||||||
- Remarque : cas d’une bobine idéale (r = 0) :
| uAB = L . | di |
|
|
|
| dt |
Établissement du courant dans une bobine. (TP Physique N° 08).
- Équation différentielle vérifiée par l’intensité i.
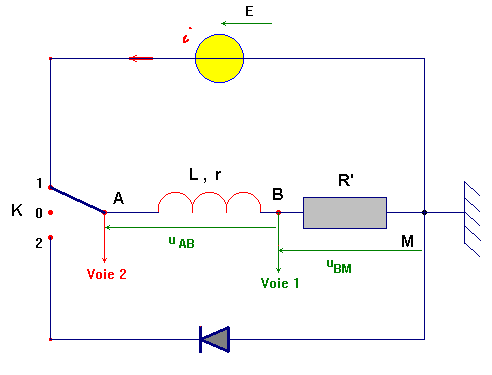
- La loi d’additivité des tensions dans le circuit série permet d’écrire :
-

- En ordonnant, on peut écrire :
-

Constante de temps du circuit.
- Expression de la constante de temps t.
- La durée de l’établissement ou de l’annulation du courant dans un circuit (R, L) dépend de la résistance R et de l’inductance L du circuit.
-
On appelle constante de temps du circuit (R,
L), la valeur
 .
.
- τ constante de temps : seconde s. R résistance du circuit ohm Ω. L inductance du circuit : henry H.
- Lors de l’établissement du courant, l’expression de l’intensité du courant électrique dans le circuit est donnée par l’expression :
-
 .
Lors de l’annulation du courant électrique dans le circuit :
.
Lors de l’annulation du courant électrique dans le circuit :

Énergie emmagasinée dans une bobine.
- Une bobine d'inductance L, traversée par un courant d’intensité i, emmagasine de l'énergie.
-
C'est de l'énergie magnétique que l'on note
|
|
Em énergie en joule (J) |
||||||
|
L inductance en henry (H) |
||||||
|
|
I intensité en ampère (A) |
8.
Oscillations libres dans un circuit (R, L, C).
![]()
Le condensateur.
|
Représentation symbolique :
|
|
La Bobine.
|
Représentation symbolique :
|
|
Le conducteur ohmique.
|
Représentation symbolique :
|
uAB = R . i |
- Selon la valeur de la résistance du circuit (R, L, C), on distingue les régimes : pseudo-périodique, critique, apériodique.
- Il existe une valeur particulière R C de la résistance R qui délimite les deux régimes. On l’appelle la résistance critique.
-
Si R <
R C
, on observe des oscillations libres amorties, c’est le régime
pseudo-périodique.
-
Si R = R
C , la tension tend rapidement vers zéro, c’est le régime critique.
-
Si R >
R C, la tension tend vers zéro sans oscillations, c’est le régime apériodique.
Étude analytique d’un circuit oscillant.
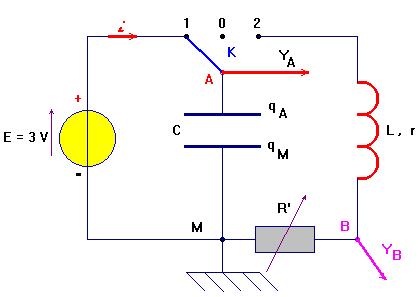
- Équation différentielle d’un circuit (R, L, C).
|
|
|
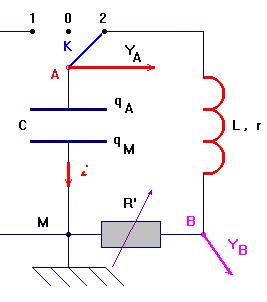
Premier temps : on charge le condensateur en basculant le commutateur sur la position1. |
 |
|
Deuxième temps : au temps t = 0, on bascule le commutateur sur la position 2. |
-
On utilise l’additivité des tensions :

- On pose : R = R’ + r et on ordonne :
-

- Durant les oscillations libres amorties, la charge q du condensateur obéit à l’équation différentielle :
-

Équation différentielle d’un circuit (L, C).
- Un circuit (L, C) est un circuit idéal de résistance nulle : R = 0.
- En conséquence, la charge q du condensateur obéit à l’équation différentielle suivante :
-

Solutions de l’équation dans le cas d’un circuit (L, C).
-
L’équation différentielle
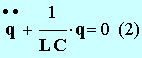 est une équation linéaire en q,
du second ordre, sans deuxième membre.
est une équation linéaire en q,
du second ordre, sans deuxième membre.
- Elle admet une solution générale de la forme :
-
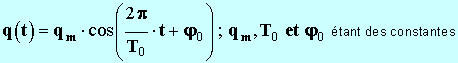
- T0 représente la période propre des oscillations.
-
Elle s’exprime en seconde s. :
![]()
- Remarque : la pseudo-période T ≈ T0 période propre si le système est peu amorti.
- Un circuit (L, C) possède deux réservoirs d’énergie entre lesquels des échanges d’énergie provoquent des oscillations électriques.
- Des échanges d’énergie se produisent entre le condensateur et la bobine.
- Les variations de WC et WL sont périodiques, de période égale à la moitié de la période propre T0 de l’oscillateur libre.
- L’énergie du condensateur et l’énergie de la bobine varient en sens inverses.
- Si l’amortissement est négligeable, l ‘énergie totale du système se conserve.
- Mais comme tout circuit électrique comporte une résistance R, l’énergie se dissipe par effet Joule.
9.
![]()
Le vecteur position, le vecteur vitesse et le vecteur accélération.
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
Les lois de Newton.
- Première loi de Newton : le principe d’inertie.
|
Dans un référentiel galiléen, si la somme vectorielle des forces extérieures qui s’exercent sur un système est égale au vecteur nul,
alors son
centre d’inertie G
est
Soit
au repos
Soit
animé d’un mouvement rectiligne uniforme.
Réciproquement, dans un référentiel galiléen,
si le centre d’inertie G d’un système est Au repos ou animé d’un mouvement rectiligne uniforme, alors la somme vectorielle des forces extérieures
qui s’exercent sur le système
est égale au vecteur nul :
(Pour le repos :
)
|
- Deuxième loi de Newton : théorème du centre d’inertie.
|
Dans un référentiel Galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse du solide par le vecteur accélération
de son centre d’inertie.
On
écrit :
si
on pose :
|
- Troisième loi de Newton : principe des actions réciproques.
|
Soient deux corps A et B.
A est situé au point O
et B
est situé au point P. Lorsqu’un corps A exerce sur un corps B une action mécanique représentée
par le vecteur force
Le corps B exerce sur un corps A une action mécanique représentée
par le vecteur force
Les
forces
|
10.
Chute verticale d’un solide.
![]()
|
La force de pesanteur est représentée par le vecteur
|
|
||||||||||||
|
Expression de
Tout corps immergé dans un fluide est soumis à une force verticale
vers le haut, de valeur égale au poids du volume V de fluide déplacé par le corps immergé.
ρ0 représente la masse volumique du fluide. Pour l’eau :
ρ
0 = 1,0
kg . dm –
3 |
|
||||||||||||
Force de frottement :
-
La force de frottement est toujours colinéaire et de sens contraire
au vecteur vitesse
![]() du
centre d’inertie du solide.
du
centre d’inertie du solide.
-
Expressions de la force de frottement ![]() .
.
- On peut distinguer deux grandes lois de variation pour la valeur de la force de frottement fluide f.
- Lorsque la vitesse limite atteinte est « faible », la force de frottement fluide est de la forme : f = k . v G
- La constante k dépend de la viscosité du fluide et de la forme du solide. C’est une grandeur positive.
- Lorsque la vitesse limite atteinte est « grande », la force de frottement fluide est de la forme : f = k . vG2
- Équation différentielle du mouvement.
 |
ρ : masse volumique du solide |
|
ρ0 : masse volumique
du fluide |
|
|
|
-

-
De l’expression (2), on tire :
![]()
- Pour obtenir une expression plus simple, on pose :
-

-
D’autre part :

Étude analytique.
- La force de frottement fluide est de la forme : f = k.v.
- On pose : vx = v et on remplace dans l’équation (4).
-

- On reconnaît une équation différentielle du premier ordre avec deuxième membre qui admet une solution du type :
-
![]() où A,
B et k1 sont
des constantes.
où A,
B et k1 sont
des constantes.
Résolution de l’équation par une méthode itérative : la méthode d’Euler.
Étude d’une chute libre verticale.
-
Définition : On appelle chute libre le mouvement d'un objet
soumis uniquement à son poids ![]() .
.
- Conséquence de l'application du théorème du centre d'inertie (deuxième loi de Newton).
-

11.
Mouvements de projectiles.
![]()
Étude préliminaire.
- Le système : la balle de masse m et de centre d'inertie G.
- Le référentiel : référentiel terrestre considéré comme galiléen car cette courte durée, on peut considérer que la terre n'a pas bougé.
-
Le repère d'espaces lié au référentiel d'étude :

- Conditions initiales :
|
|
|
Étude dynamique.
-
Bilan des forces : la balle est soumise à son poids ![]() .
.
- On peut négliger la poussée d’Archimède et les forces de frottements.
- Deuxième loi de Newton (Théorème du centre d'inertie) :
-

étude cinématique :
- équations horaires du mouvement.
- Coordonnées du vecteur accélération :
|
|
et |
|
De l’équation (1), on tire |
|
-
Coordonnées du vecteur vitesse. On utilise la relation
 .
.
- On cherche les primitives des équations précédentes. Il apparaît des constantes qui sont liées aux conditions initiales.
|
|
D’après les conditions initiales |
|
-
Coordonnées du vecteur position. On opère de la même façon :

|
|
D’après les conditions initiales |
|
Équation de la trajectoire.
- On élimine le temps t entre pour trouver la relation entre x et y : y = f (x).
|
|
On déduit l’équation de la trajectoire |
|
Les lois de Kepler.
-
Première loi : la loi des trajectoires
- Dans le référentiel héliocentrique, la trajectoire du centre d’une planète est une ellipse dont le Soleil est l’un des foyers.
- Remarque : le cercle est une ellipse dont les deux foyers sont confondus avec le centre.
-
Deuxième loi : Loi des aires.
- Le segment de droite qui relie le centre du Soleil au centre de la planète balaie des aires égales pendant des durées égales.
- Il résulte de ceci que la planète se déplace plus vite lorsqu’elle se rapproche du Soleil.
- En toute rigueur, le mouvement d’une planète n’est pas uniforme.
-
Troisième loi : Loi des périodes.
- Pour toutes les planètes, le rapport entre le cube du demi-grand axe a de la trajectoire et le carré de la période T de révolution est la même :
-
 .
.
- Cette constante ne dépend pas de la masse de la planète.
- Si la trajectoire est circulaire, on peut écrire que :
-
 .
.
Mouvements des planètes et des satellites.
- Le mouvement circulaire uniforme.
- Caractéristiques du mouvement circulaire uniforme.
- Considérons un point mobile M animé d’un mouvement circulaire uniforme.
- La trajectoire est un cercle de centre O et de rayon R et la valeur de la vitesse ne change pas au cours du temps.
- Pour simplifier l’étude d’un tel mouvement et en déduire les caractéristiques, il faut utiliser le repère de Frenet :
-

-
![]() désigne
un vecteur unitaire tangent à la trajectoire et orienté dans le sens du mouvement.
désigne
un vecteur unitaire tangent à la trajectoire et orienté dans le sens du mouvement.
-
![]() désigne
un vecteur unitaire perpendiculaire à
désigne
un vecteur unitaire perpendiculaire à ![]() et orienté vers le centre O
du cercle.
et orienté vers le centre O
du cercle.

-
Le vecteur vitesse est tangent à la trajectoire au point considéré
![]() .
.
- Le vecteur vitesse change de direction à chaque instant.
-
Le vecteur accélération peut se décomposer de la façon suivante :

- R est le rayon de la trajectoire circulaire.
- En conséquence, le vecteur accélération peut être décomposé en une :
- Accélération tangentielle qui dépend de la variation de la valeur de la vitesse.
- Accélération normale qui est liée à la variation de la direction du vecteur vitesse.
- Dans le cas d’un mouvement circulaire uniforme :
-

- L’accélération est radiale et centripète. Elle est dirigée vers le centre de la trajectoire.
Satellites terrestres.

-
Expression vectorielle de la force :

- Dans le référentiel géocentrique, on applique la deuxième loi de Newton :
-

-
Pour simplifier l’étude, on travaille dans le repère de Frenet :

-
On remarque que
![]() .
.
-
L’expression de l’accélération dans ce repère :

- Dans le référentiel géocentrique, l’accélération du centre d’inertie du satellite est indépendante de sa masse.
- Le vecteur accélération est centripète.
-
Si la trajectoire du satellite est circulaire, alors

- puisque dans le cas d’un mouvement circulaire uniforme :
- L’expression de l’accélération dans ce repère :
-

- Expression de la vitesse :
-
En identifiant :

- Dans le référentiel géocentrique, le mouvement d’un satellite en orbite circulaire est uniforme.
Expression de la période : durée nécessaire pour effectuer un tour
-

Le Satellite géostationnaire.
- Un Satellite Géostationnaire est un Satellite qui reste toujours à la verticale d’un même point P de la Terre.
- Le plan de l’orbite dans le référentiel géocentrique est le plan équatorial.
13.
Les oscillateurs mécaniques.![]()
Le pendule pesant.
- Définition : Un pendule pesant est un système oscillant en rotation autour d’un axe horizontal.
- Écarté de sa position d’équilibre, il oscille autour de cette position sous la seule action de son poids.
- Une balançoire constitue un pendule pesant.
Le pendule simple.
- Un pendule simple est constitué d’un objet de petites dimensions suspendu à un fil de masse négligeable.
- La masse du fil est négligeable devant la masse m de l’objet et la longueur du fil ℓfil > 10 R .
- R représente le rayon d’un objet sphérique.
-
Expression de la période :
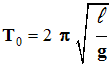
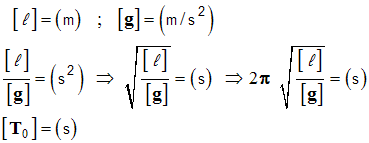
Le pendule élastique.
- Force de rappel exercée par un ressort.
- Un ressort à spires non jointives exerce une force proportionnelle à la longueur du déplacement de l’extrémité libre du ressort.
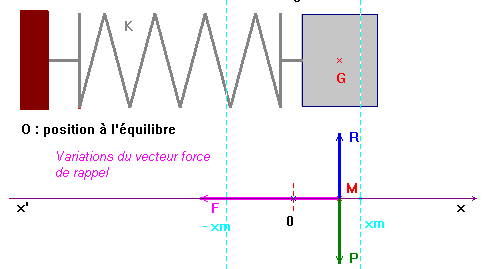
- O représente la position de l’extrémité du ressort à l’équilibre (origine de l’axe) et
- M représente la position de l’extrémité du ressort lorsqu’il est excité.
-
Force de rappel ![]() exercée
par le ressort sur le solide S :
exercée
par le ressort sur le solide S :
-
expression vectorielle :
![]()
- Valeur de la tension : F = k . | x |
Expression de la période de la période propre de l’oscillateur élastique.
-
Expression de la période propre du pendule élastique :
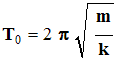
|
Le mobile est soumis : |
|
|
|
|
- Dans le référentiel terrestre supposé galiléen, on peut appliquer le théorème du centre d’inertie :
-
![]()
- Projetons la relations sur l’axe x’Ox :
-
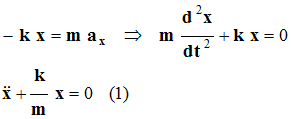
-
La solution générale de l’équation est du type :
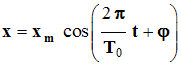
- La grandeur x m représente l’amplitude des oscillations,
- T 0 représente la période propre des oscillations et
- φ la phase à l’origine des dates.
- La période propre est liée aux caractéristiques du système mécanique.
-
La solution vérifie l’équation (1) si
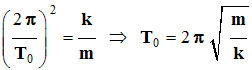
Phénomène de résonance.
- Les oscillations forcées.
|
- Définition : Un système oscillant de fréquence propre f0, que l’on appelle le résonateur, subit des oscillations forcées, s’il oscille à la fréquence f imposée par l’excitateur. |
expression du travail dans le cas général.
-
Le travail d’une force quelconque ![]() entre
A
et B
le long d’un trajet quelconque est égal à la somme de tous les travaux élémentaires
entre A
et B.
entre
A
et B
le long d’un trajet quelconque est égal à la somme de tous les travaux élémentaires
entre A
et B.
- Si le déplacement devient infiniment petit, on écrit :
-

Travail de la force appliquée à l’extrémité d’un ressort.
- La force appliquée à l’extrémité d’un ressort par un opérateur (l’autre extrémité étant fixe) est appelée tension du ressort.
-
La tension du ressort
![]() .
Avec O
position de l’extrémité du ressort à vide et
M
position de l’extrémité du ressort lorsqu’il est déformé.
.
Avec O
position de l’extrémité du ressort à vide et
M
position de l’extrémité du ressort lorsqu’il est déformé.
- On prend l’axe x’Ox pour repérer l’allongement algébrique :
-

![]()
- Calculer le travail de la tension du ressort pour passer de l’allongement xA à l’allongement xB.
-

- Comme l’allongement passe de xA à xB, la force varie au cours du déplacement.
-
Le travail se calcule en prenant une infinité de déplacements
élémentaires :
![]()
-
On en déduit l’expression du travail élémentaire effectué par
la force
![]() pour passer de l’allongement x
à l’allongement x
+ dx :
pour passer de l’allongement x
à l’allongement x
+ dx :

- Par intégration, on obtient le travail de la force :

énergie potentielle.
- Énergie potentielle de pesanteur :
|
EPP = m . g . zM |
{ |
EPP : énergie potentielle de pesanteur, joule (J) |
|
m : masse de l'objet, kilogramme (kg) |
||
|
g : accélération de la pesanteur, (m / s 2) |
||
|
z : altitude (côte) du centre d'inertie, mètre (m) |
- l’énergie potentielle de pesanteur augmente avec l’altitude.
- Il faut choisir une altitude de référence qui simplifie les calculs.
Énergie potentielle élastique.
- La variation d’énergie potentielle élastique d’un ressort est l ‘énergie transférée par un opérateur qui déforme le ressort en le faisant passer d’un allongement x A à l’allongement x B.
- Par analogie, l’énergie potentielle élastique, que possède un ressort qui est allongé ou détendu, est définie par la relation suivante :
|
|
Epe : énergie potentielle élastique en joule (J) |
||||||
|
k : constante de raideur du ressort (N / m) |
||||||
|
|
x : allongement du ressort en mètre (m) |
énergie mécanique d’un système.
- Énergie cinétique de translation.
- L’énergie cinétique de translation d’un système, de masse m et de vitesse v, dans un référentiel donné, est donnée par la relation :
|
|
EC : énergie cinétique de translation en joule (J) |
||||||
|
m : masse du système en kilogramme (kg) |
||||||
|
|
v : vitesse de traslation du système (m / s) |
- énergie mécanique d’un système S = { Solide + Ressort } horizontal :
- L’énergie mécanique Em du système S est la somme de l’énergie cinétique EC du système S et de l’énergie potentielle élastique Epe des ressorts.
|
+ |
1 2 |
k . x 2 |
- Énergie mécanique d’un projectile :
- L’énergie mécanique d’un projectile dans un champ de pesanteur uniforme est la somme de son énergie potentielle de pesanteur et de son énergie cinétique dans le référentiel d’étude.
|
+ |
m . g . z |
- Mouvement sans frottement : L’énergie mécanique se conserve :
|
+ |
m . g . z |
= |
c te |
15.
Ouverture au monde quantique.![]()
Les forces newtoniennes.
- La force gravitationnelle.
- Deux corps ponctuels A et B de masses respectives mA et mB exercent l’un sur l’autre des forces d’attraction, directement opposées, dirigées suivant la droite (AB), de valeur proportionnelle aux masses et inversement proportionnelle au carré de leur distance r.
|
- Expression vectorielle :
Schéma :
|
- G est la constante de gravitation Universelle : G ≈ 6,67 × 10 – 11 m3 . kg – 1 . s – 2
- La force électrostatique.
|
- Premier cas : on considère que : q A . q B > 0
|
|
- Deuxième cas : on considère que : q A . q B < 0
|
|
- Dans le vide, deux particules A et B, portant les charges électriques respectives qA et qB, séparées par la distance r sont soumises à deux forces directement opposées : -
- Expression :
-
vecteur unitaire : direction droite (AB) et sens de A vers B. - k
≈ 9,0
×
10 9 S.I |
Niveaux d’énergie électroniques d’un atome.
- Définition des niveaux d’énergie :
- Un atome ne peut exister que dans certains états d’énergie quantifiés, caractéristiques de l’élément.
|
-
émission : - La perte d’énergie d’un atome excité passant du niveau d’énergie Ep vers un niveau inférieur En s’accompagne de l’émission d’un photon d’énergie : - Ep - En = h . υ |
|
|
-
Absorption : - L’absorption d’énergie lumineuse par un atome ne peut se faire que si l’énergie du photon permet une transition d’un niveau En à un niveau supérieur Ep tel que : - Ep - En = h . υ |
|
- Un atome ne peut absorber que les radiations qu’il est capable d’émettre.
- Les échanges d’énergie liés aux transitions atomiques sont de l’ordre de l’électronvolt : 1 eV = 1,6 × 10 – 19 J
application : l’atome d’hydrogène.
-
L'atome d'hydrogène est constitué d'un proton et d'un électron.
Les niveaux d'énergie de l'atome sont donnés par
-

- Le nombre n est un nombre entier positif. L'état de plus basse énergie correspond à n = 1, le premier état excité à n = 2, etc.,
- n = infini correspondant à l'état ionisé: l'atome d'hydrogène a perdu son électron et il se forme l'ion H+.
Niveaux d’énergie des molécules et des noyaux.
- Les molécules.
- Les molécules sont le plus souvent constituées de plusieurs atomes.
- Dans le calcul de l’énergie d’une molécule il faut tenir compte de l’énergie de vibration, mais aussi de l’énergie de rotation.
- Les vibrations d’une molécule sont dues aux oscillations des atomes autour d’une position d’équilibre.
- Une molécule peut aussi posséder des mouvements de rotation autour de différents axes.
- Cela dépend de la géométrie de la molécule.
- Les molécules présentent des niveaux d’énergie quantifiés.
- Chaque niveau est associé à un état de vibration et de rotation donné.
- Les spectres moléculaires sont plus complexes que les spectres atomiques.
- Le spectre de raies d’absorption typique d’une molécule montre des séries de raies très proches les unes des autres.
- L’énergie correspondante à ces transitions est de l’ordre du meV.
- Avec les spectroscopes usuels dont le pouvoir de résolution est faible, les raies sont très proches les unes des autres,
- on observe des bandes noires d’absorption.
- Les noyaux.
- L’énergie des noyaux est également quantifiée.
- Un noyau peut effectuer des transitions de niveau d’énergie par émission ou absorption d’un photon.
- Un noyau peut aussi être excité par la collision avec une particule suffisamment énergétique.
- Les transitions nucléaires sont très énergétiques.
- Les énergies échangées lors des transitions sont de l’ordre du MeV.
-
Les photons émis
ou absorbés sont du domaine des rayons
γ.
- Exemple : Une désintégration radioactive s’accompagne le plus souvent de l’émission de photons γ.
- Souvent, après la désintégration, le noyau-fils se retrouve dans un état excité.
- Il se désexcite alors pour revenir dans son état fondamental par émission d’un ou plusieurs photons γ.