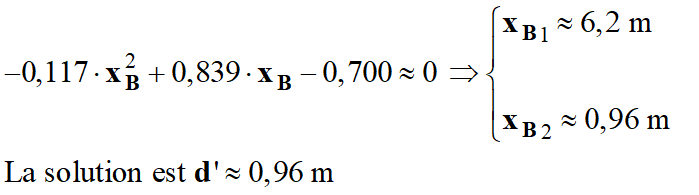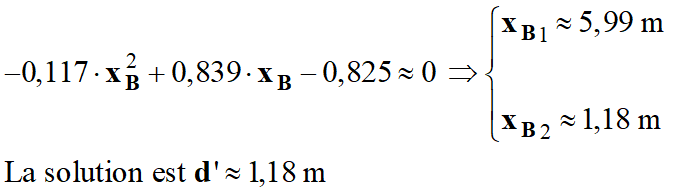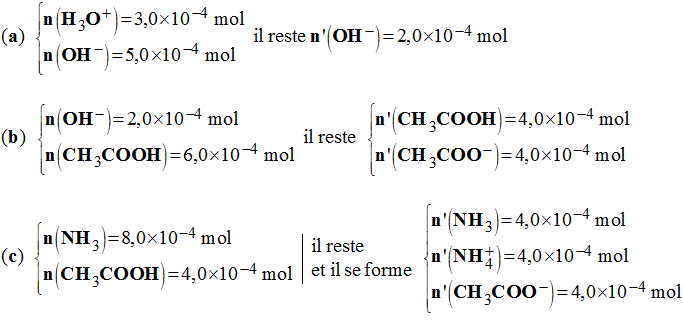I- Le contre au Basket.

 

 

 On étudie la trajectoire du centre d’inertie d’un ballon de basket-ball lancé par un joueur.

On ne teindra pas compte ni de la résistance de l’air, ni de la rotation éventuelle du ballon sur lui-même.

Le lancer est effectué vers le haut ; on lâche le ballon lorsque son centre d’inertie est en A (voir schéma).

Sa vitesse initiale est représentée par le vecteur situé dans le plan vertical et faisant un angle α avec l’axe horizontal.

 

1)- Établir les équations horaires du mouvement du centre d’inertie du ballon. En déduire l’équation de la trajectoire.

-    équations horaires du mouvement du centre d’inertie du ballon.

-    Système : le ballon ; le référentiel : Terrestre supposé Galiléen ; Conditions initiales :

-      

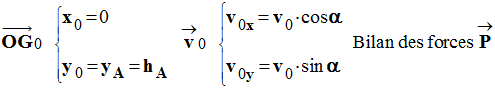
-    Théorème du centre d’inertie :

-     

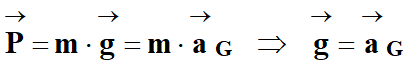
-    Par intégrations successives, on trouve :

-     

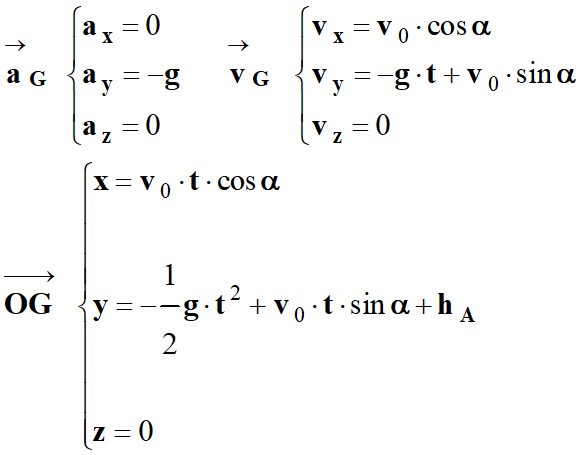
-    équation de la trajectoire : on élimine le temps entre x et y

-     

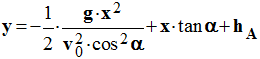
2)- Calculer la vitesse initiale du ballon, pour que celui-ci (le centre d’inertie du ballon) passe exactement par le point C, centre du panier.

-    Vitesse initiale du ballon

-    Le centre d’inertie du ballon doit passer par le point C :

-     

-     

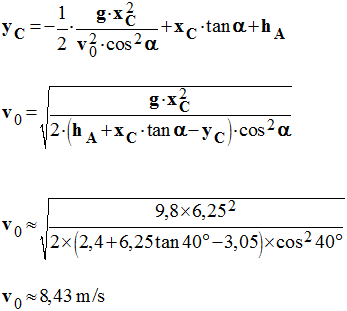
3)- Un défenseur BD, placé entre l’attaquant et le panneau de basket saute verticalement pour intercepter le ballon :

L’extrémité de sa main se trouve en B à l’altitude h_B = 3,10 m.

à quelle distance horizontale maximale d’ de l’attaquant doit-il se trouver pour toucher le ballon du bout des doigts ?

-    Données : g = 9,8 m / s2 ; α = 40 °; diamètre du ballon : 25 cm ;

-    h_A = 2,40 m ; h_B = 3,10 m ; h_C = 3,05 m ; d = 6,25 m

-    distance horizontale maximale d’ pour toucher le ballon du bout des doigts.

-    Les doigts doivent se trouver au point B de coordonnées :

-     

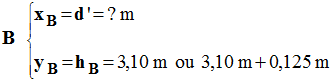
-    En reprenant l’équation :

-     

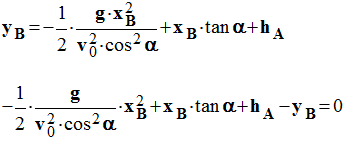
-    Il faut résoudre une équation du type :

-     

-   

 

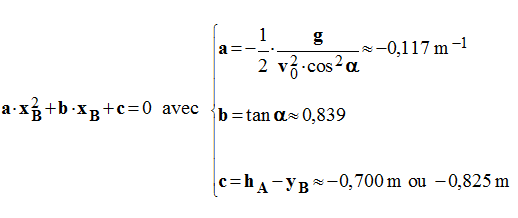
-    Ou :

II-  Réaction acide-base.

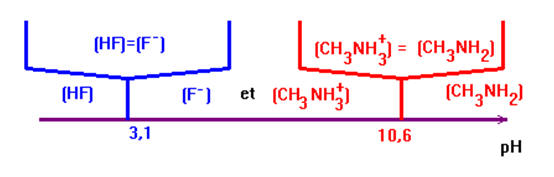
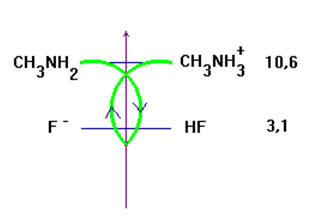
1)- Tracer les domaines de prédominance relatifs des couples HF / F^– ; pK_A1 = 3,2 et CH₃NH₃⁺ / CH₃NH₂ ; pK_A2 = 10,6.

-    Domaines de prédominances :

 

2)- On mélange 50 mL de solution d’acide fluorhydrique de concentration C = 1,0 x 10 ^{– 1} mol / L et 50 mL de solution de méthanamine de concentration C’ = 1,0 x 10 ^{– 1} mol / L.

a)-  Quelle est la réaction qui a lieu ? Calculer sa constante K_R. Conclure.

-    réaction et constante K_R. conclusion.

 

-     

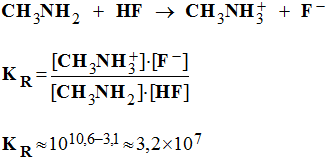
-    La réaction est quasi totale.

b)-  Quelles sont les espèces prédominantes en fin de réaction ? calculer leurs concentrations.

-    Espèces prédominantes  et concentrations :

-     

 

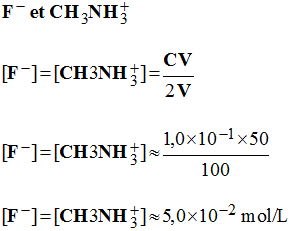
III- Il ne faut pas faire de mélange.

On mélange les solutions suivantes :

25 mL de solution d’acide chlorhydrique de concentration	C1 = 1,0 × 10 – 1 mol / L
25 mL de solution de soude de concentration	C2 = 2,0 × 10 – 2 mol / L
25 mL de solution d’acide éthanoïque de concentration	C3 = 2,4 × 10 – 2 mol / L et de pKA = 4,8
25 mL de solution aqueuse d’ammoniac de concentration	C4 = 3,2 × 10 – 2 mol / L et de pKA = 9,2

1)- Indiquer les réactions prépondérantes successives. Les qualifier.

-    Réaction prépondérantes successives :

 

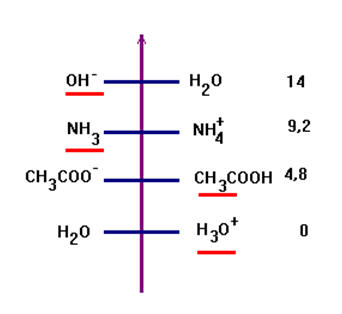
(a)            HO^–   +   H₃O⁺   →   2 H₂O

(b)           HO^–   +   CH₃COOH   →   CH₃COO^–   +    H₂O

(c)            NH₃   +   CH₃COOH   →   CH₃COO^–   +    NH₄⁺

-    Les qualifier : Les réactions sont quasi totales.

 

2)- Quel est le couple acido-basique dont les deux espèces sont majoritaires ? Justifier.

 

-    couple acido-basique dont les deux espèces sont majoritaires.

-     

-    En fin de réaction :

 

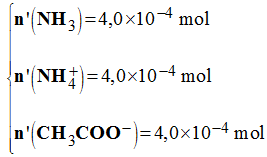
3)- En déduire la valeur du pH de la solution. Justifier.

-    valeur du pH de la solution.

-    Le pH dépend du couple :

-    NH₄⁺ / NH₃   : comme : [NH₄⁺] =[ NH₃]   =>  pH ≈ pK_A ≈ 9,2