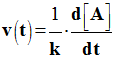|
Correction |
|
|
Exercice I : Suivi cinétique par spectrophotométrie
|
Équation |
H2O2 (aq) |
+ 2
H +(aq) |
+ 2 I – (aq) |
→ |
I2 (aq) |
+ 2
H2O
(ℓ) |
|
|
état |
Avanc. |
mol |
mol |
mol |
|
mol |
mol |
|
État initial |
0 |
n0 |
excès |
n1 |
|
0 |
excès |
|
Au
cours de la Trans. |
x (t) |
n0 – x (t) |
excès |
n1 – 2 x (t) |
|
x
(t) |
Excès |
|
Avancement max |
xmax |
n0 – x max |
excès |
n1 – 2 x max |
|
xmax |
Excès |
|
- Hypothèse 1 : On considère que le réactif limitant est l’eau oxygénée. - En conséquence : - n0 – xmax1 = 0 => n0 = xmax1 ≈ 8,0 × 10 – 5 mol - Hypothèse 2 : On considère que le réactif limitant est l’ion iodure. - En conséquence : - n1 – 2 xmax2 = 0 - n1 = 2 xmax1 ≈ 6,0 × 10 – 5 mol - xmax2 ≈ 3,0 × 10 – 5 mol - Détermination de xmax. - Conclusion : L’avancement maximal est égal à la plus petite des deux valeurs : - La réaction s’arrête lorsque l’un des réactifs a totalement disparu. - xmax = xmax2 ≈ 3,0 × 10 – 5 mol |
|
Équation |
H2O2 (aq) |
+ 2
H+(aq) |
+ 2 I – (aq) |
→ |
I2 (aq) |
+ 2
H2O
(ℓ) |
|
|
état |
Avanc. mol |
mol |
mol |
mol |
|
mol |
|
|
État initial (mol) |
0 |
n0 ≈
8,0
× 10 – 5 |
excès |
n1 ≈
6,0
× 10 – 5 |
|
0 |
excès |
|
Au
cours de
la trans |
x (t) |
n0 – x (t) |
excès |
n1 – 2 x (t) |
|
x
(t) |
Excès |
|
bilan |
xmax ≈ 3,0
× 10
– 5 |
5,0 × 10 – 5 |
excès |
0,0 |
|
3,0
× 10 – 5 |
Excès |
|
4)- Déterminer les concentrations initiales (à t = 0) en ion iodure I – et en eau oxygénée H2O2 . - Concentration initiale en eau oxygénée :
- - Concentration initiale en ions iodure :
-
5)- Calculer la valeur de la concentration en diiode en fin de réaction. - Concentration en diiode en fin de réaction :
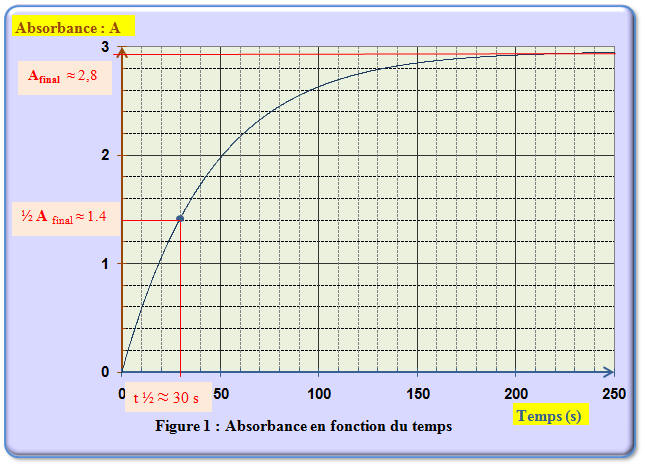
- On lance la mesure de l’absorbance en fonction du temps en effectuant une mesure toutes les secondes. On obtient l’enregistrement donné en annexe (figure 1) : 1)- Définir la vitesse volumique de réaction.
- Définition : La vitesse volumique de réaction
v (t) à
la date t, est la dérivée par
rapport au temps,
- Du rapport
entre l’avancement x de la réaction et le volume
V du
milieu réactionnel.
-
- Lorsque
l’on travaille à volume constant, on obtient la relation suivante :
- Remarque :
- La
relation : n’est valable que lorsque l’on travaille à volume constant.
2)- Déterminer l’expression de la vitesse volumique de réaction en fonction
- Pour
déterminer la valeur de la vitesse de réaction, on trace la tangente à
la courbe
[I2] =
f (t), car
-
- En conséquence :
- - Comme : A = k x [I2] avec k constante par rapport au temps
-
- 3)- Déterminer la valeur de la vitesse volumique de réaction à t = 50 s. Si nécessaire, on prendra k = 190 SI. - Valeur de la vitesse de la réaction t = 50 s.
- 4)- Comment évolue la vitesse volumique de réaction ? Donner une interprétation microscopique à ce phénomène. - La vitesse volumique de réaction est proportionnelle au coefficient directeur a de la tangente à la courbe A = f (t). - Ce coefficient directeur a diminue au cours du temps. - En conséquence, la vitesse diminue. - La vitesse d’une transformation chimique est maximale à l’instant initial. - Elle décroît ensuite et s’annule lorsque la réaction est terminée. - Les réactifs sont consommés au fur et à mesure que la réaction se poursuit. - Comme la concentration des réactifs est un facteur cinétique, la diminution de la concentration des réactifs entraîne la diminution de la vitesse. - Elle s’annule si le réactif limitant à totalement disparue. 5)- Après l’avoir défini, déterminer le temps de demi-réaction. - Le temps de demi-réaction, noté t1/2, est la durée au bout de laquelle l’avancement de la réaction est égal à la moitié de sa valeur finale. - Le temps de demi-réaction fournit une échelle des temps caractéristique du système étudié. - L’expérience montre qu’un système siège d’une réaction caractérisée par le temps de réaction t1/2 - cesse pratiquement d’évoluer au bout d’une durée de l’ordre de quelques t1/2 (4 à 7 suivant la précision recherchée). - Le temps de demi-réaction permet d’évaluer la durée nécessaire à l’achèvement de la transformation chimique étudiée. - Valeur du temps de demi-réaction : - Avancement final : xfinal = xmax2 ≈ 3,0 × 10 – 5 mol - ½ x final ≈ 1,5 × 10 – 5 mol - Valeur correspondante de l’absorbance : - A ≈ 190 [I2]
- - Remarque : - on peut considérer que lorsque l’avancement est égal à la moitié de - l’avancement final, - l’absorbance est égale à la moitié de l’absorbance finale. - Car A ≈ 190 [I2]
6)- Cette réaction s’est déroulée à une température θ. Donner l’allure de la courbe A = f (t) sur le graphe fourni si elle s’était déroulée à une température θ’ inférieure à θ.
|
ANNEXE A RENDRE AVEC
Suivi cinétique par spectrophotométrie






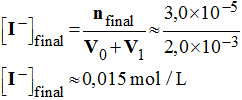

 de
puis de
de
puis de


 .
.