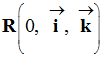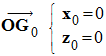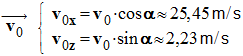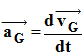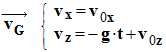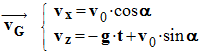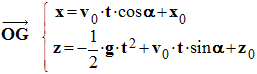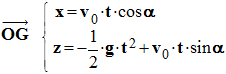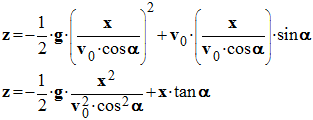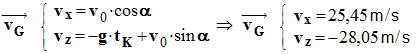I- Exercice 1 :    Saut à skis idéal (4 pts)

À la date t = 0 s, un skieur émerge d’un tremplin à la vitesse  de valeur 92 km / h, inclinée d’un angle  α = 5 ° sur l’horizontale.

On considère le mouvement du centre d’inertie G du skieur en ne prenant pas en compte les actions de l’air sur le système.

1)- Le skieur est-il en chute libre lorsqu’il a franchi le tremplin ? Pourquoi ?

- Le système : le skieur ; le référentiel d’étude est le tremplin (référentiel terrestre supposé Galiléen) ;

- Bilan des forces : le poids du skieur  ; la poussée d’Archimède  ; les forces de frottement .

- Comme on ne prend pas en compte les actions de l’air sur le système, le skieur est soumis à la seule action de son poids.

- Par définition, il est en chute libre.

2)- établir les expressions littérales des équations horaires du mouvement de G dans le repère .

- On applique la deuxième loi de Newton :

- Énoncé :

-  Dans un référentiel Galiléen, la somme vectorielle des forces extérieures appliquées à un solide

est égale au produit de la masse du solide par le vecteur accélération de son centre d’inertie. On écrit :

-  (1)

- Coordonnées du vecteur accélération :

- Conditions initiales :

- Coordonnées du vecteur vitesse. On utilise la relation :

- 

-  On cherche les primitives des équations précédentes.

- Il apparaît des constantes qui sont liées aux conditions initiales.

- Coordonnées du vecteur position. On opère de la même façon :

- 

3)- En déduire l’équation de la trajectoire.

- On élimine le temps t entre pour trouver la relation entre x et y : y = f(x).

- La trajectoire de G est une portion de parabole contenue dans un plan vertical contenant le vecteur vitesse .

4)- Soit K la position de G au moment où le skieur retombe sur la piste. La dénivellation entre O et K est de 40 m.

a)- Calculer la durée t_K du saut.

- durée t_K du saut.

- On connaît la côte z _K = – 40 m. Il faut résoudre l’équation :

- 

- On remplace g, v₀ et sin α par leurs valeurs respectives et en simplifiant, on obtient l’équation du second degré  :

 – 4,9 t_K²  + 2,23 t_K  + 40 = 0.

- Cette équation admet deux solutions : t’ ≈ 3,09 s et t’’ ≈ – 2,64 s.

- Avec l’origine des dates choisie, la bonne solution est : t_K ≈ 3,09 s.

b)-  En déduire la valeur de la coordonnée x _K du point K.

- On utilise le fait que

- x_K = v ₀. t_K . sin α  =>  x_K ≈ 25,45 x 3.09  =>  x_K ≈ 78,6 m 

c)-  Calculer la valeur de la vitesse de G à l’instant où il arrive en K et l’angle de ce vecteur avec l’horizontale.

-  Valeur de la vitesse au point K :

- 

- 

-  Valeur de l’angle α_K :

- 

- La bonne solution est : α_K ≈ – 48 °

5)- En compétition, les valeurs de x _K sont supérieurs à 100 m Pourquoi ?

- En compétition, il se peut que v₀ soit plus grand et ou α plus grand aussi ;

- x_K = v₀. t_K . sin α .

- D’autre part, il faut tenir compte des actions de l’air sur le skieur : le skieur ‘’plane’’, il s’appuie sur l’air.

Données : valeur du champ de pesanteur : g = 9,8 m / s².