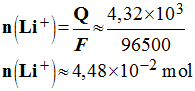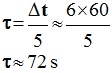|
Antilles 2011 :
Bac Sciences Physiques Exercice 2 : Pile au Lithium et
supercondensateur (5,5 pts)
Énoncé et correction |
|
|
|
|
Exercice N°
02 : Pile au lithium et supercondensateur (5,5 pts) |
Exercice N° 02 : Pile au lithium et supercondensateur (5,5 pts)
|
Un sondage réalisé en ligne auprès de 1873 personnes du 22 au 27 septembre 2010, révèle que 65% des français seraient prêts à acheter une voiture électrique et ce pourcentage atteint même 72% si l’on considère la tranche des 25-34 ans. Ce sondage s'intéresse également à l'échéance d'achat. Il souligne une donnée importante : 64% des personnes interrogées sont prêtes à acheter un véhicule électrique d'ici 5 à 10 ans ! Cependant, la première raison qui bloque les Français à opter pour la voiture électrique est le nombre encore insuffisant de bornes de recharge (92% des personnes interrogées). Dans ce contexte, les constructeurs doivent donc en priorité gérer le délicat problème du stockage de l'énergie électrique de leurs véhicules. Aujourd'hui deux grandes tendances semblent se dessiner : l'utilisation de batteries au lithium et celle de supercondensateurs. Nous nous proposons d'étudier ces 2 technologies. |
1.
PARTIE 1 : Accumulateur au Lithium
|
Un accumulateur est un système chimique qui fonctionne comme une pile (générateur), lorsqu'il se décharge et qui a la possibilité d'être rechargé comme une batterie de voiture classique (d'où le nom impropre de « pile rechargeable ») ; il se comporte alors comme un récepteur. Les recherches actuelles pour les véhicules électriques tendent à utiliser des accumulateurs « Li-ion » dans lesquels l'élément lithium est apporté sous forme ionique par le composé LiFePO4. La tension de fonctionnement de ces accumulateurs est de l'ordre de UPN = 3,3 V. Leur temps de recharge a été considérablement diminué mais reste malgré tout encore environ de trois heures.
1.1. On s'intéresse d'abord à la «recharge» de
l'accumulateur sur lequel le fabriquant a indiqué une quantité
d'électricité Q = 4,32 kC. 1.1.1. Après avoir donné les expressions littérales, déterminer la valeur de l'intensité du courant nécessaire à cette recharge, si elle s'effectuait pendant une durée Δt = 20 s.
1.1.2. Les valeurs d'intensité de courant usuellement utilisées au laboratoire permettraient-elles une durée de recharge aussi courte ?
1.2. On s'intéresse maintenant à la «décharge» de l'accumulateur. 1.2.1. L'ion lithium appartient au couple Li + (aq) / Li (aq) et constitue la borne positive de l'accumulateur. Écrire l'équation de la réaction qui se produit à cette électrode, et donner le nom de cette électrode.
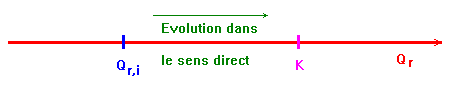
1.2.2. La transformation qui se produit dans la pile est-elle spontanée ou forcée ? (La nature de cette transformation n'est pas demandée). Au cours du fonctionnement de la pile le quotient de réaction est-il supérieur ou inférieur à la constante d'équilibre de la réaction qui a lieu au sein de l'accumulateur ?
1.2.3. En considérant la décharge totale de l'accumulateur, calculer la quantité d'ions Li + consommée.
Données : 1
F = 96500 C :
M (Li)
= 7,0 g . mol –1 |
||||||||||||||||||||||||||
2. PARTIE 2 : Le Supercondensateur
|
Le supercondensateur implanté dans un véhicule électrique se différencie d'un condensateur électrochimique classique par sa capacité à accumuler une grande quantité d'énergie (par exemple pendant les phases de freinage et d'accélération). Ils sont donc capables d'envoyer à un appareil électrique une puissance élevée pendant un temps court, ce que ne permet pas une batterie. Ces supercondensateurs stockent une quantité d'énergie plus faible qu'une batterie mais ils la restituent plus rapidement. Ils ont une durée de vie plus longue, peuvent fonctionner dans des conditions de températures plus extrêmes et sont plus légers, plus faciles à entreposer et à entretenir. Ils
peuvent se recharger en Δt = 6,0
min.
Pour étudier un tel condensateur de capacité C, on le monte dans un circuit en série avec un conducteur ohmique de résistance R = 1,0 Ω. On considérera qu'à l'instant t = 0, date de basculement de l'interrupteur de la position 1 à la position 2, le condensateur est totalement chargé sous une tension E = 2,5 V.
2.1. Rappeler l’expression de la constante de temps τ d'un circuit RC et montrer, par une analyse dimensionnelle, que τ est homogène à un temps.
2.2. On considère que le condensateur a été totalement chargé après une durée Δt = 5 t. En déduire la valeur de t puis celle de la capacité C de ce condensateur. Cette valeur de capacité est-elle fréquemment rencontrée au laboratoire ? Le circuit est orienté dans le sens du courant précisé dans le schéma ci-dessus : le condensateur et le conducteur ohmique sont alors en convention récepteur.
2.3. Rappeler la relation qui lie l'intensité i (t) à la dérivée de la charge q (t) par rapport au temps.
2.4. En appliquant la loi des tensions à ce circuit, établir l'équation différentielle vérifiée par la tension uC (t).
2.5. La solution de cette équation est de la forme uC (t) = A.e – t . β. Déterminer : 2.5.1. L'expression de β ;
2.5.2. L'expression de A ;
2.5.3. L'expression finale de uC (t).
2.6. Donner l'expression littérale de i (t) en fonction de E, R et C. Quel est le sens réel du courant pendant la décharge du condensateur ?
|