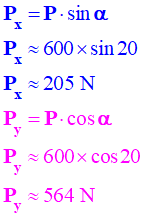|
Phys. N° 03 Action mécanique et vecteur force . Exercices |
|
|
|
|
I-
Exercice : connaissances essentielles.
II-
Exercice 12 page 65.
III-
Exercice 17 page 66.
IV-
Exercice 19 page 67.
V-
Exercice 22 page 67.
VI-
Exercice 27 page 68. |
I- Exercice : connaissances essentielles.
|
Connaissances essentielles. 1)- Quels peuvent être les effets d’une action mécanique exercée sur un corps ? 2)- Trouver l’origine de la modification du mouvement : a)- D’une balle qui rebondit sur le sol : b)- D’un parachute qui ne tombe pas verticalement : c)- D’une boule sur un billard : 3)- Trouver l’origine de la déformation : a)- D’une voile de bateau : b)- De la corde d’un arc : c)- D’un ballon que l’on gonfle : 4)- Classer par actions réparties et actions localisées. a)- Action du vent sur la voile : b)- Action de l’eau sur un barrage : c)- Action d’un filin sur un bateau : d)- Action de la pointe d’un stylo sur une feuille : e)- Coup de pied sur un ballon : 5)- Énoncer les caractéristiques d’une force. 6)- Choisir la bonne réponse : La valeur d’une force est mesurée : a)- Par un manomètre : b)- Un dynamomètre : c)- Un baromètre : d)- Un newtonmètre : L’unité de force est : e)- Le pascal : f)- Le kilogramme : g)- Le bar : h)- Le newton : VRAI. 7)- Énoncer la condition d’équilibre d’un solide soumis à deux forces :
8)-
Quelle est la
relation entre l’intensité (ou valeur) F
de la force
pressante
qui s’exerce sur une
surface S perpendiculaire à
Préciser l’unité de chaque grandeur. 9)- Définir le poids d’un corps soumis à des forces de pesanteur : |
|
Connaissances essentielles. 1)- Quels peuvent être les effets d’une action mécanique exercée sur un corps ? - Une action mécanique ou force est capable de : - Déformer un corps ou - De le mettre en mouvement ou de modifier son mouvement. 2)- Trouver l’origine de la modification du mouvement : a)- D’une balle qui rebondit sur le sol : - Réaction du sol au moment de l’impact. b)- D’un parachute qui ne tombe pas verticalement : - Action du vent sur le parachute. c)- D’une boule sur un billard : - Choc entre la boule et une paroi du billard ou choc de la boule avec une autre boule. 3)- Trouver l’origine de la déformation : a)- D’une voile de bateau : - La force pressante exercée par le vent sur la voile. b)- De la corde d’un arc : - Main de l’archer sur la corde. c)- D’un ballon que l’on gonfle : - Force pressante exercée par l’air sur la paroi du ballon. 4)- Classer par actions réparties et actions localisées. a)- Action du vent sur la voile : - Action répartie sur la surface de la voile. b)- Action de l’eau sur un barrage : - Action répartie sur la surface du barrage. c)- Action d’un filin sur un bateau : - Action localisée. d)- Action de la pointe d’un stylo sur une feuille : - Action localisée. e)- Coup de pied sur un ballon : - Action répartie sur la surface de la chaussure. 5)- Énoncer les caractéristiques d’une force.
6)- Choisir la bonne réponse : La valeur d’une force est mesurée : a)- Par un manomètre : (FAUX : un manomètre mesure une pression) b)- Un dynamomètre : VRAI c)- Un baromètre : (FAUX : un baromètre mesure une pression) d)- Un newtonmètre : FAUX L’unité de force est : e)- Le pascal : FAUX c’est une unité de pression du système international f)- Le kilogramme : FAUX c’est l’unité de masse. g)- Le bar : FAUX c’est une unité de pression h)- Le newton : VRAI. 7)- Énoncer la condition d’équilibre d’un solide soumis à deux forces :
-
- Les deux forces sont égales et opposées et elles ont la même ligne d’action.
8)-
Quelle est la
relation entre l’intensité (ou valeur) F
de la force
pressante
qui s’exerce sur une
surface S perpendiculaire à
Préciser l’unité de chaque grandeur.
9)- Définir le poids d’un corps soumis à des forces de pesanteur :
|
II- Exercice 12 page 65. Représentation d’une force localisée
|
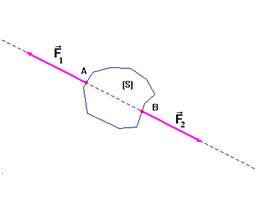
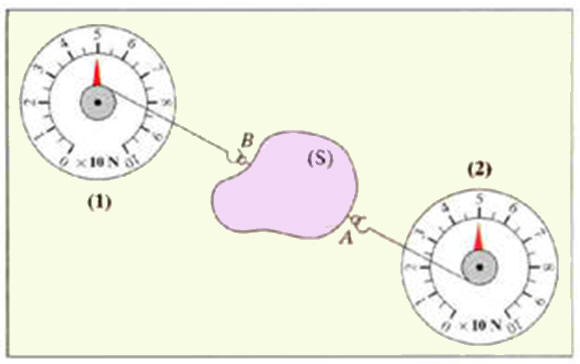
Représentation d’une force localisée
1)- Reproduire le schéma ci-dessous et
représenter : -
la force exercée par
A sur le solide
S ; - la
force exercée par B
sur le solide S ; -
Échelle : 1 cm ↔ 10 N. 2)- le solide S peut-il être en
équilibre dans ces conditions ? On négligera le poids du solide S par
rapport à l’intensité Des autres forces.
|
|
Représentation d’une force localisée
1)- Représentation des forces. Chaque force est représentée par un segment fléché de 5 cm de longueur.
2)- Conditions d'équilibre. - Le solide S est en équilibre car il est soumis à deux forces : - Dont la somme vectorielle est égal au vecteur nul :
-
- Et dont les droites d'action sont confondues. |
III- Exercice 17 page 66. Portance et traînée d’une aile d’avion
|
Portance et traînée d'une aile d'avion. Lorsqu’une aile d’avion est en
mouvement avec une vitesse
Voir le schéma ci-dessous.
On appelle portance
1)- Représenter graphiquement la
portance
2)- Exprimer
F et
T en fonction de
R et
α, sachant que lorsque
α est petit, On peut écrire sin
α ≈
α et cos
α ≈ 1 avec
α en radian. 3)- Calculer
F et
T avec
R = 3000 N et
α = 8°. 4)- Calculer la finesse
f de l’aile
définie par le rapport
F /
T. |
|
Portance et traînée d'une aile d'avion. Voir le schéma ci-dessous.
1)- Représentation graphique.
2)- relations : - F = R . cos α ≈ R si l'angle α est petit en radians - T = R . sin α ≈ R.α si α est petit en radians 3)- Valeurs :
-
4)- Finesse de l'aile d'avion :
-
|
IV- Exercice 19 page 67. Coordonnées d'un vecteur force
|
Coordonnées d'un vecteur force 1)- Dans un repère dont les axes
On a représenté un vecteur force
On peut écrire :
Déterminer
Fx et
Fy. 2)- Exprimer l’intensité
F de la force
Donner la valeur numérique de
F. 3)- Exprimer le sinus de l’angle
4)- Exprimer la tangente de l’angle
α en fonction de
Fx et
Fy. |
|
Coordonnées d'un vecteur force
1)- Schéma :
2)- Fx ≈ 3,0 N et Fy ≈ 2,0 N
-
3)- et 4)- Relations :
-
|
V- Exercice 22 page 67. Coordonnées du vecteur poids.
|
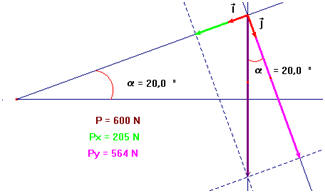
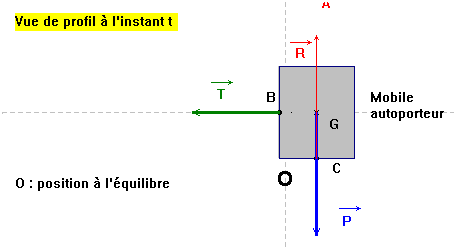
Coordonnées du vecteur poids. Une luge descend une pente enneigée
inclinée d’un angle
α Par rapport au plan horizontal. Déterminer dans le repère
Les coordonnées du poids
On prendra
α = 20 ° et
P = 600 N.
|
|
Coordonnées du vecteur poids. On prendra
α = 20 ° et
P = 600 N.
-
|
VI- Exercice 27 page 68. Corps flottant
|
Corps flottant Un iceberg a un
volume émergé Ve = 600 m3. Sa masse volumique est
ρ1 =
910 kg.m – 3, celle de l’eau de mer est
ρm = 1024 kg.m – 3. 1)- Schématiser l’iceberg flottant
et préciser les forces auxquelles il est soumis lorsqu’il
est en équilibre. 2)- Écrire la condition d’équilibre.
Trouver une relation Entre le volume émergé
Ve, le
volume total Vt
et les
Masses volumiques
ρ1 et
ρm. 3)- Calculer le volume
Vt et
la masse de l’iceberg. |
|
Corps flottant 1)- Schéma :
2)- Condition d’équilibre : - Poussée d'Archimède : - Elle est égale au poids du volume d'eau de mer déplacée :
-
F = mm
. g = ρm
. Vi
. g
-
F = mm .
g = ρm . (Vt - Ve).
g (1) - Poids de l'Iceberg :
-
P = m . g
-
P = ρi .
Vt . g
(2) 3)- Volume total de l'Iceberg : - En combinant (1) et (2) :
-
|
|
|
|
|
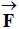



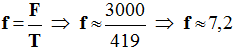
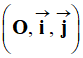 sont gradués en N,
sont gradués en N,  (schéma
ci-dessous)
(schéma
ci-dessous)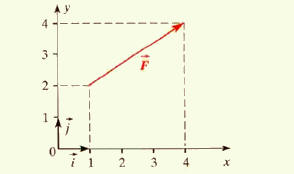
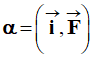 en fonction de
Fy et
F.
en fonction de
Fy et
F.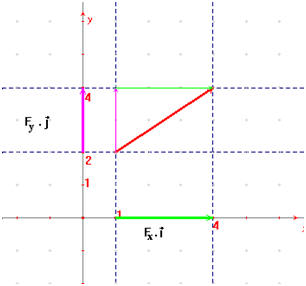
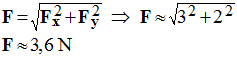
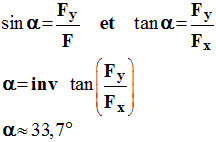
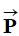 .
.