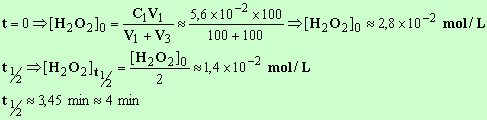Vitesse d'une réaction chimique. Correction |
|
|
|
1)- Introduction.
|
On étudie la réaction entre les ions iodure et l'eau oxygénée en milieu acide qui est lente à la température ambiante. Le diiode apparu est dosé par une solution titrée de thiosulfate de sodium en présence d'un indicateur : l'empois d'amidon. |
2)- Expérience 1 :
Réaction entre les ions iodure et l'eau oxygénée en milieu acide.
- A l'instant t = 0, 0 s, On verse :
|
A l'instant t = 0, 0 s, on verse :
|
||
|
Dans un erlenmeyer de 250 mL |
3)- Expérience 2 :
|
Dosage du diiode formé au temps t. - Dans une burette graduée de
25 mL,
- on introduit
une solution titrée de thiosulfate de sodium de
concentration C2
= 4,0 × 10 –2 mol / L
-
et on règle le zéro de la graduation.
- On prépare un bécher contenant
50 mL
d'eau glacée environ et quelques gouttes d'empois d'amidon.
- Grâce à une pipette jaugée, on
prélève un volume V0 = 10 mL du
mélange réactionnel.
- On verse le contenu de la
pipette dans un erlenmeyer de 250 mL.
- Au temps ti = 1 min, on verse le contenu du
bécher dans l'erlenmeyer pour arrêter la
réaction.
-
On dose ensuite le diiode formé à
la date ti.
- Pour ce faire, on verse progressivement la solution de
thiosulfate de sodium
(contenue dans la burette graduée)
dans l'erlenmeyer.
- Une coloration bleu noir doit apparaître.
- On ajoute goutte à goutte le thiosulfate de sodium
jusqu'à décoloration de la solution.
- On note le volume de solution de thiosulfate de sodium
versé
- V2 =
- On recommence l'expérience au temps
ti
= 2 min, puis
tj
= |
4)- Tableau de mesures.
|
Temps t min |
V2
mL |
[I2]
mol / L |
[H2O2]
mol / L |
|
0 |
0,00 |
0,0000 |
0,0280 |
|
1 |
2,40 |
0,0048 |
0,0232 |
|
2 |
4,40 |
0,0088 |
0,0192 |
|
4 |
7,40 |
0,0148 |
0,0132 |
|
6 |
8,90 |
0,0178 |
0,0102 |
|
8 |
9,70 |
0,0194 |
0,0086 |
|
10 |
10,30 |
0,0206 |
0,0074 |
|
12 |
10,90 |
0,0218 |
0,0062 |
|
14 |
11,20 |
0,0224 |
0,0056 |
|
16 |
11,40 |
0,0228 |
0,0052 |
|
18 |
11,60 |
0,0232 |
0,0048 |
|
20 |
11,80 |
0,0236 |
0,0044 |
|
24 |
11,90 |
0,0238 |
0,0042 |
|
28 |
11,90 |
0,0238 |
0,0042 |
|
32 |
12,00 |
0,0240 |
0,0040 |
|
36 |
12,10 |
0,0242 |
0,0038 |
|
40 |
12,20 |
0,0244 |
0,0036 |
1)- Étude thermodynamique.
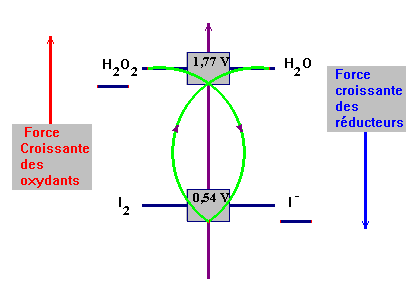
- On donne les potentiels standard des deux couples mis en jeu :
|
H2O2
/ H2O
E01
= 1,77 V |
I2
/ I –
E03
= 0,54 V |
|
- demi-équations électroniques des différents couples et équation bilan de la réaction.
- Qualificatifs : réaction naturelle ou spontanée, lente, unique, totale. - Réactif limitant et réactif en excès. - Quantité de matière d'eau oxygénée à l'instant initial :
-
n0H2O2 =
C1 .
V1 ≈ 5,6
× 10
–3 mol - Quantité de matière d'ion iodure à l'instant initial : -
n0I– =
C3 .
V3 ≈ 2,0
× 10–2
mol - or :
n0I– >
2 n0H2O2 ;
I – est en excès et
H2O2
est en défaut.
|
2)- Exploitation de la réaction
de dosage.
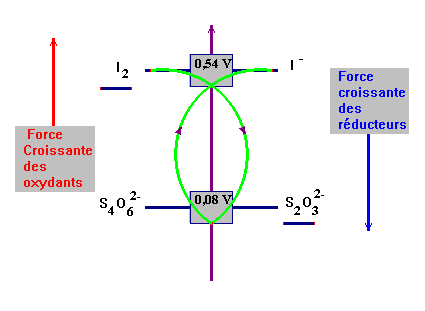
- On donne les potentiels standards des deux couples mis en jeu
:
I2
/ I–
- Écrire les demi-équations électroniques
des différents couples et équation bilan de la
réaction :
I2
+ 2 e –
2 I –
2 S2O32–
S4O62–
+
2 e –
2 S2O32
+ I2
→
S4O62–
+ 2 I – -
Qualificatifs : réaction naturelle ou
spontanée, rapide, unique, totale.
- Relation :
[I2 Lors du dosage, au virage de l'indicateur (l'empois
d'amidon), on est à l'équivalence,
les
réactifs sont dans les proportions
stœchiométriques, définies par les coefficients de la réaction.
- Relation :
3)- Exploitation des
mesures.
[I
![]()
![]()
![]()
![]()
![]()
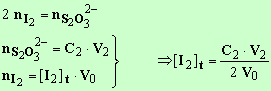
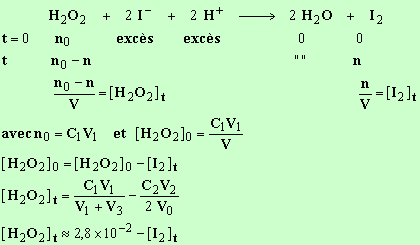
4)- Vitesse de formation du
diiode.
- Caractéristiques de la courbe obtenue : fonction
croissante du temps, au départ la variation est rapide puis
plus lente.
- La courbe tend vers une asymptote horizontale: la
réaction est finie.
- Vitesse moyenne de formation du diiode entre
t1 et
t2
- Expression de la vitesse instantanée de formation du
diiode au temps t.
- Vitesse instantanée au temps
t1 = 6 min. - Elle est numériquement égale à la valeur du coefficient
directeur de la tangente à la courbe au point M1
d'abscisse t1.
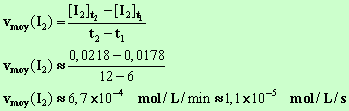
![]()
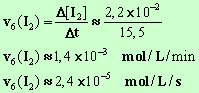
- Vitesse instantanée au temps
t = 12 min.
- Elle est numériquement égale à la valeur du coefficient directeur de la tangente à la courbe au point M2 d'abscisse t2.
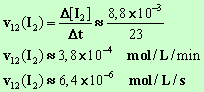
5)- Vitesse de disparition de l'eau
oxygénée.
- Caractéristiques de la courbe obtenue :
- fonction
décroissante du temps, au départ la variation est
rapide puis plus lente.
- La courbe tend vers une asymptote
horizontale : la réaction est finie.
- Expression et valeur de la vitesse moyenne de disparition de
l'eau oxygénée entre t1 et
t2.
-
- Expression de la vitesse instantanée de formation du
diiode au temps t.
-
- Vitesse
instantanée au temps t1 = 6 min : - Elle
est numériquement égale à l'opposé de la valeur du coefficient directeur de la
tangente à la courbe au point M1
d'abscisse t1. - On trace la tangente à la
courbe au point d’abscisse t2
= 12 min et on calcule la valeur du coefficient directeur de cette tangente.
- La valeur de la vitesse
est numériquement égale à l’opposée de la valeur du coefficient directeur. - v6
(H2O2) = v6
(I2)
-
v6
(H2O2)
≈ 1,4
× 10 –3 mol / L / min
-
v6
(H2O2)
≈ 2,4
× 10 –5 mol / L / s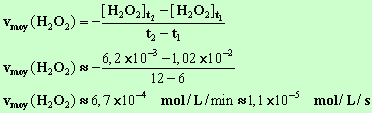
![]()
- Vitesse
instantanée au temps t2
= 12 min.
- Elle
est numériquement égale à l'opposé de la valeur du coefficient directeur de la
tangente à la courbe au point M2
d'abscisse t2.
- On trace la
tangente à la courbe au point d’abscisse t2
= 12 min et on calcule la valeur du coefficient directeur de cette
tangente.
- La valeur de la vitesse
est numériquement égale à l’opposée de la valeur du coefficient directeur.
- On
peut utiliser le fait que : d’après le bilan de quantité de matière de la
réaction chimique,
-
v12
(H2O2)
= v12 (I2)
-
v12
(H2O2)
≈ 3,8
× 10 –4 mol / L / min
-
v12
(H2O2)
≈ 6,4
× 10 –6 mol / L / s
6)- Calculer le temps de demi-réaction.
C'est la durée au bout de laquelle la moitié du réactif en défaut a disparu.