I - But. II - Inlfuence de la position de la sonde de Hall. 1)- Expérience. 2)- Schéma du montage. 3)- Mesures. 4)- Exploitation des mesures. II - Influence de l'intensité et du nombre de spires. 1)- Expérience. 2)- Schéma du montage. 3)- Mesures.

I- But.

-  Le but des expériences proposées est d'étudier les caractéristiques du champ magnétique créé par une bobine longue (le solénoïde) parcourue par un courant.

II- Influence de la position de la sonde de Hall.

1)- Expérience :

On étudie le champ magnétique créé par un solénoïde parcouru par un courant continu, d'intensité I = 3,0 A.

On mesure la valeur de ce champ magnétique B en différents points de l'axe x'Ox du solénoïde.

2)- Faire le schéma du montage.

3)- Mesures :

-  Reproduire et compléter le tableau.

-  Tableau  de mesures groupe G₁ :

4)- Exploitation des mesures :

- Tracer le courbe B = f (x) prendre les échelles suivantes :

- Abscisses : 1 cm <==>2 cm

- ordonnées : 4 cm <==>1 mT

- Comment sont les lignes de champ à l'intérieur du solénoïde ?

- Quelle conclusion peut-on tirer de l'allure du graphe ?

- Remarque : on peut faire une étude graphique rapide à la calculatrice.

- Graphe : B = f (x)

Cliquer sur l'image pour l'agrandir

-  À l’intérieur du solénoïde, les lignes de champ sont parallèles à l’axe du solénoïde.

-  Le champ magnétique à l’intérieur d’un solénoïde est pratiquement uniforme.

III- Influence de l'intensité et du nombre de spires.

1)- Expérience.

-  La sonde du Teslamètre est placée au point O (centre du solénoïde).

-  On mesure la valeur B₀ du champ magnétique en ce point pour différentes valeurs de l'intensité I du courant.

-  On utilise l'enroulement S₁, puis l'enroulements S₂.

2)- Schéma du montage :

3)- Mesures :

-  Reproduire et compléter les tableaux suivants

-  Enroulement S₁.

-  Enroulement S₂.

4)- Exploitation des mesures :

-  On utilise la calculatrice en mode statistique et on réalise un ajustement linéaire.

-  Montrer que le modèle linéaire B₀ = k₁.I est le mieux adapté

-  Les points sont sensiblement alignés. La droite moyenne passe par l’origine.

-  Le modèle linéaire B₀ = k₁ . I est le mieux adapté.

-  On peut utiliser le tableur Excel pour exploiter statistiquement la série de mesures.

-  On sélectionne la série de données du graphique.

-  Puis on fait un clic droit pour que la fenêtre suivante s’affiche.

-  On sélectionne « Ajouter une courbe de tendance », on choisit le modèle « linéaire ».

-  On coche :

-  « Afficher l’équation sur le graphique »

-  « Afficher le coefficient de détermination (R²) sur le graphique.

-  Graphique obtenu :

-  En déduire la valeur de k₁ et son unité.

-  Valeur de k₁ et son unité :

-  Modèle mathématique : y ≈ a . x

-  Modèle physique : B₀ = k₁ . I

-  En conséquence : k₁  = a ≈ 0,6199 mT / A

-  k₁ ≈ 6,20 x 10 ^{– 4}  T / A

-  Donner la valeur du coefficient de corrélation R et conclure.

-  Valeur du coefficient de corrélation R :

-  Le coefficient de corrélation permet de savoir si le modèle choisit est en adéquation avec la représentation graphique obtenue.

-  R² ≈0,9999  =>   R ≈ 0,99995 ≈ 1,0

-  Il y a dépendance statistique entre les variables x et y (c’est-à-dire I et B)

-  Le modèle choisi est bien en accord avec les valeurs expérimentales.

-  Montrer que le modèle linéaire B₀ = k₂.I est le mieux adapté :

-  Les points sont sensiblement alignés. La droite moyenne passe par l’origine.

-  Le modèle linéaire B₀ = k₂ . I est le mieux adapté.

-  On peut utiliser le tableur Excel pour exploiter statistiquement la série de mesures.

-  On sélectionne la série de données du graphique.

-  Puis on fait un clic droit pour que la fenêtre suivante s’affiche.

Cliquer sur l'image pour l'agrandir

-  On sélectionne « Ajouter une courbe de tendance », on choisit le modèle « linéaire ».

-  On coche :

-  « Afficher l’équation sur le graphique »

-  « Afficher le coefficient de détermination (R²) sur le graphique.

Cliquer sur l'image pour l'agrandir

-  Puis on met en forme.

-  On obtient le graphique suivant :

Cliquer sur l'image pour l'agrandir

-  En déduire la valeur de k₂ et son unité.

-  Valeur de k₂ et son unité :

-  Modèle mathématique : y ≈ a . x

-  Modèle physique : B₀ = k₂ . I

-  En conséquence : k₂  = a ≈ 1,2574 mT / A

-  k₂ ≈ 1,25 x 10^–3  T / A

-  Donner la valeur du coefficient de corrélation R et conclure.

-  Valeur du coefficient de corrélation R :

-  Le coefficient de corrélation permet de savoir si le modèle choisit est en adéquation avec la représentation graphique obtenue.

-  R² ≈0,9999  =>   R ≈ 0,99995 ≈ 1,0

-  Il y a dépendance statistique entre les variables x et y (c’est-à-dire I et B)

-  Le modèle choisi est bien en accord avec les valeurs expérimentales.

-  Que peut-on dire des grandeurs B et I à l'intérieur du solénoïde pour chaque enroulement ?

-  Les grandeurs B et I à l'intérieur du solénoïde sont proportionnelles.

-  Graphe :

Cliquer sur l'image pour l'agrandir

5)- Détermination de la relation entre B, I et n.

-  Déterminer la valeur n₁ du nombre de spires par mètre pour l'enroulement S₁.

-  n₁ ≈ 485 spires / m

-  Déterminer la valeur n₂ du nombre de spires par mètre pour l'enroulement S₂.

-  n₂ ≈ 971 spires / m

-  Comparer le rapport des coefficients k₁ et k₂ à celui des nombre n₁ et n₂. Quelle conclusion peut-on tirer ?

-  k₁ ≈ 6,20 x 10^–4  T / A  et   k₂ ≈ 1,25 x 10^–3  T / A

- 

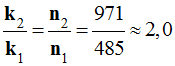
-  Montrer que B = μ.I.n.

-  On tire :

-  k₁ = μ . n₁ et k₂ = μ . n₂

-  Pour l'enroulement S₁ : B = μ.I.n₁.

-  Pour l'enroulement S₂ : B = μ.I.n₂.

-  Donner une valeur de μ en utilisant les résultats expérimentaux.

-  Valeur de μ :

-  Avec k₁ ≈ 6,20 x 10 ^{– 4}  T / A

- 

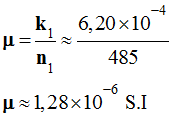
-  Avec : k₂ ≈ 1,25 x 10 ^{– 3}  T / A

- 

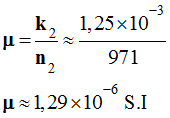
-  Calculer l'écart relatif entre la valeur expérimentale et la valeur théorique : μ₀ = 4 π x 10^–7 S . I

-  Écart relatif :

- 

6)- Récapitulatif :

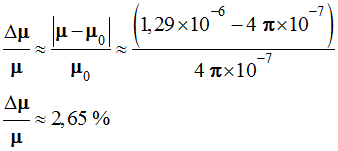
-  Faire un schéma du solénoïde en indiquant, le sens du courant.

-  Représenter les lignes de champ à l'intérieur et à l'extérieur du solénoïde.

-  Représenter le vecteur champ magnétique l'intérieur et à l'extérieur du solénoïde en différents endroits.

- Indiquer les faces du solénoïde.

-  Le solénoïde :

-  Le champ magnétique à l’intérieur d’un solénoïde est pratiquement uniforme.

-  Les lignes de champ à l’intérieur du solénoïde sont des droites parallèles.

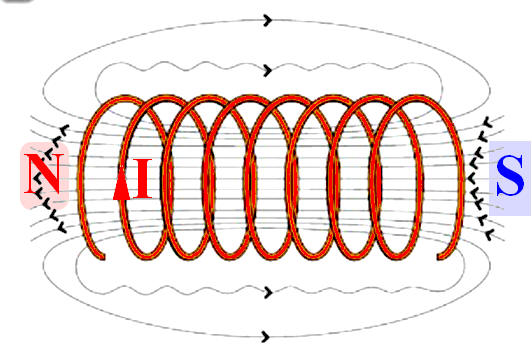
Champ magnétique dans un solémoïde

-  Caractéristiques du vecteur champ magnétique.

Simulation : animation en CabriJava permettant de simuler

les mesures effectuées à l'aide du teslamètre

(Solénoïdemesure.fig).