|
|
|
|
|
|
|
|
III-
Interférences
lumineuses. |
- Le rayon lumineux est l’outil fondamental en optique géométrique.
-
On utilise le principe de propagation
rectiligne de la lumière.
- Il est très utile pour trouver l’image d’un objet donnée par un instrument d’optique.
-
Il permet
d’expliquer les phénomènes de réflexion et de réfraction.
-
En fait pour nous, le rayon lumineux est
un faisceau parallèle très étroit.

|
Loi de la Réflexion |
Loi de la Réfraction |
|
i1 = r |
n1. sin i1 = n2. sin i2 |
-
La lumière se propage en ligne droite
dans tout milieu transparent homogène et isotrope.
2)-
Limite de l’optique géométrique. Expériences : phénomène de diffraction.
-
La question que l’on peut se poser :
Peut-on isoler un rayon lumineux ?
- Expérience : un faisceau cylindrique de lumière rouge émis par un laser est envoyé sur une ouverture circulaire.
-
La lumière rouge émise par le
laser Hélium-néon
a les caractéristiques suivantes :
|
Longueur d'onde dans le vide et l'air |
Fréquence |
|
λ0 ; 633 nm |
ν = 4,74 x 1014 Hz |
-
Premier cas : l
>> λ
Si le
diamètre du trou est grand devant la longueur d’onde, on obtient sur l’écran une
tache de même diamètre que le trou.
Le trou
a diaphragmé la lumière.
La propagation rectiligne de
la lumière est respectée.
-
Deuxième cas :
l
= λ .
Si le
diamètre du trou est du même ordre de grandeur que la longueur d’onde,
on
observe sur l’écran une tache circulaire, nettement plus grande que le trou et
entourée d’anneaux alternativement noirs et brillants.
La
tache brillante centrale est appelée : tache d’AIRY.
Expérience complémentaire :
diffraction du faisceau laser par une fente et diffraction par un réseau.
- On dit que la lumière a été diffractée par le trou.
- Il est impossible d’isoler un rayon lumineux. Le rayon lumineux n’est qu’un modèle bien utile.
- Les phénomènes de diffraction se manifestent d’autant plus que les ouvertures qui limitent les faisceaux sont petites.
- A cause de ce phénomène, on ne peut pas isoler un rayon lumineux.
- Le phénomène de diffraction est caractéristique des ondes. La lumière se propage sous forme d’ondes.
II-
Modèle ondulatoire de la lumière.
1)- Propriétés des ondes lumineuses.
- Une vitesse de propagation ou célérité qui dépend du milieu de propagation.
- La lumière se déplace dans le vide à la vitesse : c = 3,0 x 108 m . s−1.
-
Dans un milieu transparent d’indice
n ,
 avec
n > 1
.
avec
n > 1
.
- Une périodicité temporelle
T
, la période qui s'exprime en
s
.
- Une périodicité spatiale
λ
, la longueur d’onde en
m.
- A un instant donné, les signaux sont le
même état physique s’ils sont placés à des distances
d
,
d
+
λ
, d + n
λ
de la source.
-
Relation fondamentale :
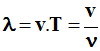
-
λ
est la longueur d’onde en
m
,
v
est la vitesse de l’onde dans le milieu de propagation et
T
la période en
.
- Remarque : dans le vide :
λ0 =
c . T
et dans le milieu d’indice
n,
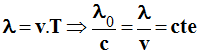
- La longueur d’onde dépend du milieu
de propagation.
La période et de ce fait la fréquence ne dépendent pas du milieu de propagation.
La fréquence n est une grandeur caractéristique de la radiation lumineuse.
III-
Interférences
lumineuses.
|
|
La tache de diffraction est striée de fines bandes rectilignes noires, parallèles, équidistantes et perpendiculaires à la direction S1 et
S2. |
- Au
phénomène de diffraction se superpose le phénomène d’interférence.
- L’ensemble des
franges alternativement brillantes et sombres constitue des franges
d’interférences.
- La
distance entre deux franges sombres ou brillantes est la même.
- On l’appelle
l’interfrange, noté i.
-
On utilise les ultrasons pour mettre en évidence ce phénomène
qui est caractéristique des ondes.
- Dispositif expérimental :

Première étape : seul l’émetteur
E1
est en marche. On déplace le récepteur
R.
- Lorsque
l’on éloigne le récepteur R,
les courbes se décalent l’une par rapport à l’autre.
-
Lorsque les courbes sont en phase, cela veut dire que les points sont dans le
même état vibratoire.
-
Pour que les courbes soient de nouveau en phase, il faut déplacer le récepteur
de la distance d,
égale à une longueur d’onde λ.
-
Deuxième étape : seul l’émetteur
E2 est en marche. On
déplace le récepteur R.
- Idem.
- Troisième
étape : les deux émetteurs E1
et E2 sont
en marche.
-
On déplace le récepteur R
le long d’une
droite perpendiculaire à (E1,
E2).
-
On constate qu’en certains points, l’amplitude est maximale et qu’en d’autres
points, l’amplitude est minimale.
-
Si on place le récepteur à un endroit ou
l’amplitude est maximale et que l’on arrête E2,
on remarque que la vibration émise par E1et
en phase avec celle reçue par le récepteur.
- On
recommence, mais maintenant, on arrête
E1.
On fait la même remarque.
- En
conséquence, lorsque l’amplitude est maximale, les vibrations émises par E1
et
E2
arrivent au récepteur en phase : elles
ajoutent leurs effets.
- Quatrième
étape : on place le récepteur en un point ou l’amplitude est minimale.
-
Idem.
- Lorsque
l’amplitude est minimale, les vibrations sont en opposition de phase : elles
annulent leurs effets.
- Différence de marche et chemin optique :
- On définit le chemin optique comme le produit de l’indice
n
du milieu de réfraction par la distance e
parcourue par le rayon lumineux dans le milieu. :
-
Le chemin optique (d) = n . e
-
La différence de marche
δ entre 2 ondes est égale à
la différence de leur chemin optique :
-
δ
= (d2) – (d1) = n2
. e2 – n1 . e1
-
Avec : (d1)
= n . (SS1 + S1M)
-
Et : (d2) =
n . (SS2 + S2M)
-
Avec n
= 1, on écrit : δ = |(SS2
+ S2M) –
(SS1 + S1M)|
|
|
Si les deux rayons lumineux se déplacent dans le même milieu d’indice n, il existe une différence de chemin optique entre les deux rayons. On parle de différence de marche δ. Il existe entre les deux ondes lumineuses arrivant en M une différence de marche δ. δ = |(SS2 + S2M) – (SS1 + S1M)| |
- Si δ = k . λ, , les deux ondes arrivent au point M en phase et elles ajoutent leurs effets.
- On dit que l’interférence est constructive.
- On obtient une frange
brillante.
- Si
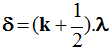 , les deux ondes arrivent au point M en opposition de phase et elles
annulent leurs effets.
, les deux ondes arrivent au point M en opposition de phase et elles
annulent leurs effets.
- On dit que l’interférence est destructive. On obtient
une frange sombre.
4)-
Nécessité
de sources cohérentes.
- pour obtenir des interférences, les sources doivent être cohérentes.
- Elles doivent être synchrones et présenter un déphasage constant.
- En optique deux sources lumineuses indépendantes ne sont jamais cohérentes.
- C’est pour cela que pour
observer des franges d’interférences, on utilise deus sources secondaires
obtenues à partir d’une source unique de petite dimension.
- Les faisceaux émis par 2 sources indépendantes ne peuvent pas interférer.
- On réalise 2 sources mutuellement cohérentes en éclairant 2 fentes avec un faisceau émis par une source primaire de petite dimension ou avec un faisceau laser.
IV-
Les
ondes électromagnétiques.
La lumière est constituée d’ondes électromagnétiques. Le domaine du visible : 400 nm ≤ λ ≤ 780 nm
a)- Description.
-
Il est apparu vers 1960. Il a été construit par Harold MAIMAN.
- L.A.S.E.R :
light amplification by stimulated emission of radiation : amplification de
lumière par émission simulée de rayonnement.
- Il existe de nombreux laser : des lasers à gaz, à cristaux, à liquides, à colorants.
- Ils sont tous construits sur le même principe.
- Un laser comprend :
- Une cavité qui contient le milieu actif dans lequel
a lieu l’émission
de lumière.
- Une source d’énergie extérieure pour entretenir l’émission.
- Un ensemble de deux miroirs rigoureusement parallèles dont l’un
est partiellement réfléchissant pour permettre l’émergence du faisceau
laser.
b)- Caractéristiques de la lumière laser.
Un faisceau laser est :
- Directif, intense monochromatique et cohérent.
- Il est très directif : le diamètre de la tache sur l’écran augmente très légèrement lorsque l’on éloigne celui-ci.
- Il est peu
divergent.
- Ce sont des sources de lumière très intenses.
- Par exemple, le
laser hélium-néon a une puissance
P
≈ 2,0 mW.
- Le rayon du faisceau émis : r ≈ 0,40 mm .
- La puissance par unité de surface :
 .
.
- Cette puissance est quatre fois supérieure à la puissance maximale du rayonnement solaire par unité de surface.
- Les faisceaux lasers sont
dangereux pour les yeux.
- La lumière laser est monochromatique.
- Elle ne peut pas être décomposée
par un prisme ou un réseau.
- La lumière laser possède une grande cohérence spatiale et
temporelle.
c)- Utilisation :
- alignements, télémétrie, usinage de métaux, fusion nucléaire, holographie,
- télécommunications, chirurgie, médecine…
2)-
Sujet Nathan 96 sujet L3 page 128. Le lecteur de compact disque.
-
Différence des distances parcourues par les
rayons de type 1 et 2.
-
Distance parcourue par les rayons de type1 : e1
= 2 e’.
-
Distance parcourue par les rayons de type2 : e2
= 2 e’ + 2 e.
-
Différence de distance : d = e2
– e1 = 2 e
-
Chemin optique :
-
(d1) = 2 e’ . nair
-
(d2)
= 2 e’ . nair + 2 n . e
-
Différence de marche :
-
δ
= (d2) – (d1) = 2 n . e – n1
. e1
-
Source laser monochromatique
- Longueur d’onde du rayonnement dans le milieu d’indice n.
- 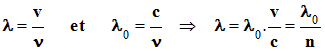
-
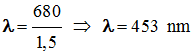
- Condition d’interférence constructive entre les rayons 1 et 2 en fonction de λ puis de λ0.
-
δ
= n . d

-
En conséquence :
-
2 e . n = k .
λ0
-
Condition d’interférence constructive entre les
rayons 1 et 2 en fonction de δ
et de λ0.
-
Or δ
= n . d et d = 2 e
Þ δ = k
. λ0.
-
C’est la condition d’interférence constructive.
-
Condition d’interférence destructrice.
-

-
Remarque : δ est appelé différence de
chemin optique dans le matériau d’indice n.
-
La plus petite épaisseur emin
qui puisse donner une interférence destructive est donnée par :
-
 ,
,
-
C’est-à-dire pour :
-

-
Application numérique :
-
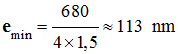
-
Si le faisceau est totalement réfléchi par la
surface du disque ou par le fond de la cuvette, il n’y a pas d’interférence,
l’éclairement est uniforme.
-
Il y a un seul type de rayon.
-
Le faisceau de lecture a un diamètre
ε, la surface éclairée par
le faisceau est :
-
Si le faisceau est totalement réfléchi par la
surface du disque ou par le fond de la cuvette, il n’y a pas d’interférence,
l’éclairement est uniforme.
-
Il y a un seul type de rayon.
-
Le faisceau de lecture a un diamètre
ε, la surface éclairée par
le faisceau est :
-
 .
.
-
La plus petite surface pour une cuvette :
-
si s < S1, s ne
peut donner lieu à aucune interférence, elle ne sera pas détectée
-
 .
.
-
Application numérique :
-
 .
.
-
Le spot est toujours centré sur une piste gravée,
l’écart l entre 2 pistes adjacentes est plus grand que le rayon
![]() de la tache lumineuse
de la tache lumineuse
![]() .
.