I- Oscillateur élastique libre peu amorti.

1)- Caractéristiques des oscillations.

-  Écarté de sa position d’équilibre et abandonné à lui-même, le solide S, en translation effectue des oscillations libres.

-  Le mobile S se déplace sur coussin d’air et on peut considérer que les frottements sont négligeables.

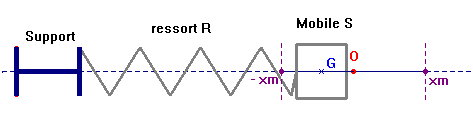
-  Le système  {support - ressort - solide } constitue un oscillateur libre.

-  L’étude de la variation de l’élongation x en fonction du temps t, x = f (t), montre que les oscillations sont sinusoïdales :

-  x = x_m cos (ω₀ . t + φ)

-  x_m  : amplitude des oscillations ( mètre m)

-  φ  : phase à l’origine des dates ( radian rad)

-  ω₀ . t + φ  : phase à l’instant t ( radian rad)

-  ω₀  : pulsation propre.

-  Remarque   :   la période propre est indépendante de l’amplitude x_m.

-  L’amplitude x_m et la phase φ à l’origine des dates sont liées aux conditions initiales.

2)- Raideur et tension d’un ressort.

-  Un ressort à spires non jointives exerce une force proportionnelle à la longueur du déplacement de l’extrémité libre du ressort.

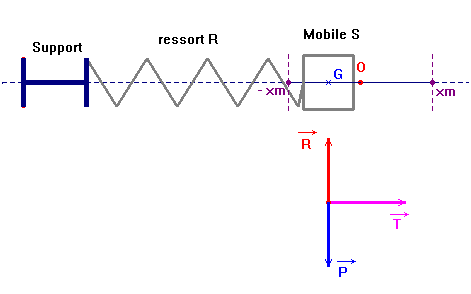
-  O représente la position de l’extrémité du ressort à l’équilibre et M représente la position de l’extrémité du ressort lorsqu’il est excité.

-  Tension exercée par le ressort sur le solide S :

-  Expression vectorielle :

- 

-  Valeur de la tension : T = k . x

-  k représente la raideur du ressort à spires non jointives en N / m,

-  x représente l’allongement du ressort par rapport à sa position d’équilibre, en m,

-  T représente la valeur de la tension en N.

3)- Expression de la période de la période propre de l’oscillateur élastique.

a)-  Période de l’oscillateur et masse du solide S.

-  On conserve le même ressort et on fait varier la masse m du solide.

-  On peut prendre m = 50 g et m = 100 g.

-  On remarque que la période T₀ augmente lorsque la valeur de la masse augmente.

-  L’étude de la courbe T₀² = f (m) montre que le carré de la période propre est proportionnel T₀ à la valeur de la masse m.

-  .

4)- Période et raideur du ressort.

-  On conserve la même masse m mais on change le ressort.

-  On prend des ressorts de différentes raideurs.

-  La période T₀ diminue lorsque la valeur de la raideur du ressort augmente.

-  L’étude de la courbe : 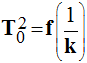montre que le carré de la période propre T₀ est inversement proportionnel à la raideur k du ressort .

-   

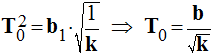
b)-  Analyse dimensionnelle.

-  Conclusion :

-   

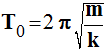
-  Montrer que cette relation a bien la dimension d’un temps.

-   

5)- étude énergétique.

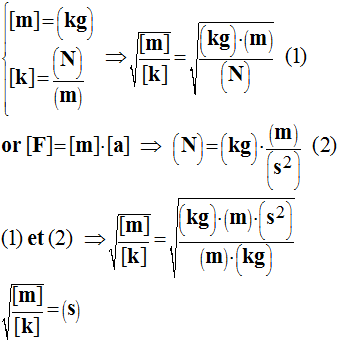
a)-  L’énergie mécanique du système S = { Terre – objet – ressort – support} :

-  E_M = E_P + E_C

b)-  L’énergie potentielle :

-  Elle comporte deux termes,

-  L’énergie potentielle de pesanteur : E_PP = m . g . h + cte.

-  Comme le pendule élastique effectue des oscillations horizontales, l’altitude du solide ne varie pas.

-  En conséquence : E_PP =  cte.

-  En prenant cette horizontale comme référence, on peut adopter : E_PP =  cte = 0.

-  L’énergie potentielle élastique liée à la déformation du ressort.

-  L’énergie potentielle élastique d’un ressort de raideur k est proportionnelle au carré de son allongement x.

-   

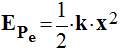
c)-  L’énergie cinétique.

-  Dans le référentiel Terrestre, le système possède l’énergie cinétique suivante (on néglige la masse du ressort devant celle du solide) :

-  .

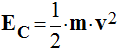d)-  Conservation de l’énergie.

-  On néglige les frottements solides et les frottements fluides (résistance de l’air).

-  L’énergie mécanique d’un oscillateur non amorti se conserve :

-   

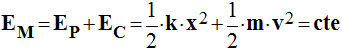
-  Cette constante dépend des conditions initiales de lancement (vitesse et amplitude).

-  Au cours des oscillations, il y a transformation mutuelle d’énergie cinétique en énergie potentielle (et inversement).

-  Remarque le système étudié : S = { Terre – objet – ressort – support} est isolé (énergétiquement).

II- Le pendule simple peu amorti.

1)- Présentation.

-  Un pendule simple est constitué d’un objet sphérique de masse m suspendu à un fil inextensible de longueur ℓ.

-  Remarque : la masse du fil est négligeable devant celle de l’objet.

-  La longueur ℓ est grande devant celle de l’objet.

-  Dans le cas contraire, on dit que le pendule est pesant.

2)- Tension du fil.

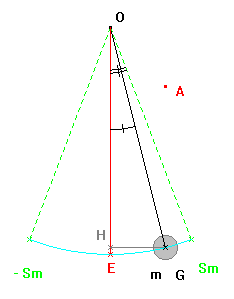
a)-  Étude à l’équilibre : exprimer la valeur de la tension T exercée par le fil sur l’objet de masse m.

-  À l’équilibre, le solide de masse m est soumis à des forces dont les effets se compensent.

-  Le centre d’inertie du solide est immobile, la réciproque du principe de l’inertie permet d’écrire que :

-   

b)-  étude lorsque le solide est en mouvement.

-  On écarte le solide de sa position d’équilibre d’un angle θ₀ < 10°.

-  On laisse le pendule osciller librement et on fait une représentation à un temps t quelconque.

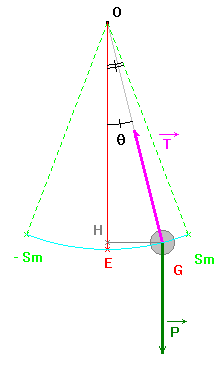
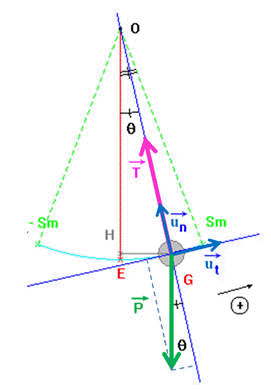
-  Expression de la valeur de la tension T en fonction de θ, v, m et g à l’instant t.

-  On travail dans le repère de Frenet :

-   

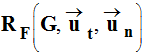
-  On donne les coordonnées de chaque vecteur force dans ce repère :

-   

-  Le théorème du centre d’inertie permet d’écrire :

- 

3)- Période propre et paramètres spécifiques.

-  La période propre des oscillations de faibles amplitudes dépend :

-  De la longueur ℓ du pendule simple

-  De la valeur g du champ de gravitation.

-  Les grandeurs ℓ et g sont des paramètres spécifiques.

-  Remarque : la période propre T₀ ne dépend pas de la masse m du solide.

-   

4)- étude énergétique.

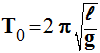
-  Considérons le système : S = { Terre – objet – fil – support} .

-  Si l’on néglige la résistance de l’air, ce système est isolé du point de vue énergétique (il n’échange pas de travail, ni de chaleur avec le milieu extérieur).

-  Son énergie mécanique se conserve, elle reste constante.

-  E_M = E_P + E_C = cte

-  énergie cinétique : dans le référentiel terrestre le mobile se déplace à la vitesse v :

-   

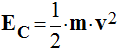
-  Energie potentielle : l’altitude du centre d’inertie de l’objet varie au cours du temps.

-  L’énergie potentielle du système S varie au cours du temps : E_P = m . g . h + cte.

-  En adoptant comme niveau de référence, le plan horizontal contenant la position d’équilibre du point G de l’objet.

-   

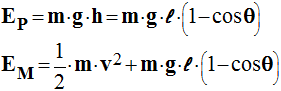
-  Durant les oscillations, il y a transformation mutuelle d’énergie cinétique en énergie potentielle.

III- Oscillations libres amorties.

1)- Amortissement fluide.

-  Les oscillations d’un pendule élastique ou d’un pendule simple s’amortissent et finissent toujours par disparaître.

-  Il y a toujours des frottements.

-  Les frottements dus à l’air (à un gaz ou à un fluide) sont des frottements fluides qui produisent un amortissement fluide.

-  Lorsque l’amortissement n’est pas trop important, le mouvement est dit pseudo-périodique : T ≈ T₀ mais T > T₀.

Simulation avec le tableur Excel

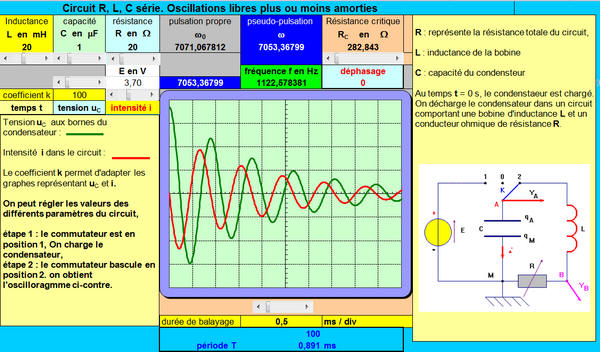
Oscillations libres (compressé)

-  La durée au bout de laquelle les oscillations ont pratiquement disparus est donnée par la relation : Δt = Q . T₀.

-  Q représente le coefficient de qualité caractéristique de l’oscillateur.

2)- Amortissement solide.

-  L’amplitude des oscillations décroît linéairement au cours du temps.

-  Si l’amortissement est trop grand, on n’observe plus d’oscillations.

-  Le mouvement n’est plus oscillatoire.