|
Phys.
N° 05 : |
|
 |
|
II- Travail et puissance d'une force.
1)- Expression du travail d'une force
constante. |
1)-
Les différentes formes d'énergie.
-
Considérons le
système S. Il possède l'énergie
E :
E =
EM
+ Umic
-
E =
EM
+ Umic
- EM : Énergie mécanique, c'est la somme de l'énergie cinétique macroscopique et de l'énergie potentielle macroscopique :
- EM = EC + EP
-
Umic :
Énergie microscopique interne.
-
C'est la somme
des énergies d'agitation (énergie cinétique microscopique, énergie potentielle
microscopique, énergies d'interaction intermoléculaire, intramoléculaire).
-
Remarque :
l'énergie cinétique dépend du référentiel d'étude.
-
Soit le système
S qui n'est pas isolé, sa variation d'énergie est due à des transferts
d'énergie :
-
Sous forme de
travail mécanique ou électrique : W
-
Sous forme de
rayonnement ou de chaleur : Q
Le principe de conservation
de l'énergie permet d'écrire : ΔE =
W +
Q
-
Énergie cinétique
d'un solide S de masse
m et de centre d'inertie
G :
.
-
Énergie
potentielle de pesanteur : EP =
m g
zG
+ cte.
II-
Travail et puissance d'une force.
1)-
Expression du travail d'une force constante.
-
Considérons une
force 
constante en direction, sens et
grandeur, dont le point d'application a un déplacement rectiligne
AB.
-
Cette force
est appliquée en un point
M d'un
solide S.
-
Le travail
mécanique 
, transféré au solide
S
par la force constante
, lorsque son point
d'application se déplace de A à
B, est égal au produit scalaire du
vecteur force par le vecteur déplacement
.
-
-
Dans le cas
présent : 
-
Unités :
en Joule
J
-
F
en Newton N
-
AB
en mètre m
-
Travail moteur.
-
Travail résistant.
2)-
Travail du poids d'un corps.
-
Considérons un
solide S de masse
m et de centre d'inertie
G se déplaçant
dans un champ de pesanteur uniforme
.
-
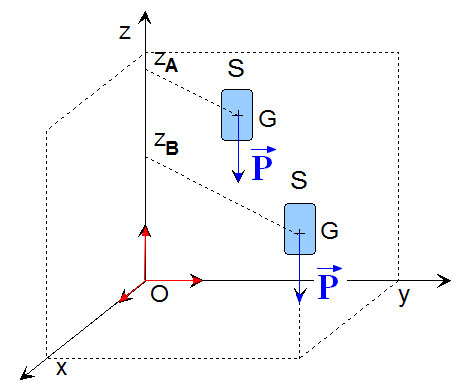
La définition du
travail mécanique d'une force constante s'applique dans ce cas.
-
Dans le repère choisi, on peut exprimer
les coordonnées de chaque vecteur :
-
En conséquence :
-
Le travail du
poids d'un corps transféré à un objet ne dépend que de la différence d'altitude
de son centre d'inertie.
-
Remarque : le
travail du poids est l'opposé de la variation de l'énergie potentielle de
pesanteur du système {terre - Solide}
-
3)-
Travail d'une force électrique constante.
-
Soit un
condensateur plan chargé :
-
On considère une
particule de charge q >
0 qui se déplace de
A vers B
sur une trajectoire rectiligne ou quelconque.
-
Le champ
électrique est uniforme à l'intérieur du condensateur et la charge
q est
soumise à une force constante
.
- On peut
calculer le travail transféré à la particule par la force électrique.
-
-
-
En conséquence,
le travail transféré à la particule dépend de la différence de potentiel entre
les points A et
B mais ne dépend pas du chemin suivi.
-
Unités :
en Joule J
-
q
en coulomb C
-
UAB
en Volt V
- Une autre unité : si q est exprimé en unité de charge élémentaire e et UAB en volt, le travail électrique W s'exprime en eV :
- 1 eV = 1,6 x 10 – 19 J
III-
Théorème de l'énergie cinétique.
Dans un
référentiel galiléen, la variation de l'énergie cinétique d'un solide en
translation entre deux instants t1 et t2 est égale à la
somme des travaux de toutes les forces extérieures appliquées au solide entre
ces 2 instants.
-
-
Considérons un
mobile autoporteur de masse m et de centre d'inertie
G se
déplaçant sur un plan incliné d'un angle α par rapport à l'horizontale.
-
Le mobile est
animé d'un mouvement de translation suivant la ligne de plus grande pente.
-
Étudions ce
mobile aux instants t1 et
t2.
-
Bilan des forces
: 
,
.
-
Schéma :
|
Instant t1 |
Position 1 |
Déplacement |
Instant t2 |
Position 2 |
|
|
|
|||
|
|
|
-
Théorème de
l'énergie cinétique :
-
IV-
Autre expression du théorème de l'énergie
cinétique.
a)-
Puissance moyenne.
-
La puissance
moyenne est égale au rapport du travail mécanique transféré par la durée du
transfert :
-
-
L'unité de
puissance est le watt symbole W.
-
Le travail d'une
force est donné par la relation :
-
,
-
représentant
le vecteur déplacement du vecteur force
.
-
En conséquence :
b)-
Puissance instantanée.
-
Par définition,
la puissance instantanée à l'instant t est égale à la dérivée par rapport
au temps du travail transféré :
-
-
La puissance
instantanée d'une force est égale au produit scalaire du vecteur force par le
vecteur vitesse de son point d'application à l'instant considéré :
-
-
Unité : puissance
P en watt (W), Force
F en newton
(N) et vitesse
v
en m / s.
2)-
Autre expression du théorème de l'énergie
cinétique.
-
Nous avons vu que
à une variation d'énergie cinétique correspond un travail mécanique :
-
-
ΔEC
correspond à la variation d'énergie cinétique entre deux instants
t1
et t2.
-
Si l'intervalle
de temps est très court, c'est-à-dire si t2 tend vers
t1,
à une variation infinitésimale de l'énergie cinétique correspond un transfert
infinitésimal du travail des forces extérieures.
La dérivée par
rapport au temps de l'énergie cinétique EC d'un solide est égale à la puissance mécanique des forces
extérieures appliquées au solide :
-
- Un pendule est constitué d'une bille de masse m de dimensions négligeables et d'un fil de longueur L et de masse négligeable.
-
On suspend ce pendule à une
potence et il est en position d'équilibre.
-
On écarte maintenant
le pendule, fil tendu d'un angle θ0 par rapport à la
verticale et on le lâche sans vitesse initiale.
-
Faire un schéma du
dispositif à un instant t
quelconque.
-
Déterminer la valeur
de la vitesse v de la bille lorsque le pendule passe par sa position
d'équilibre.
-
Déterminer la valeur
v' de la vitesse lorsque l'abscisse angulaire du pendule comptée par
rapport à la verticale a pour valeur θ.
-
On donne : θ0
= 60 ° m
= 200 g
L = 1
m
θ0
= 30 °
|
|
|
|
