|
Chap. N°
9
Réflexion et Réfraction Cours Exercices |
|
|
|

I- Étude expérimentale des lois de la réflexion (TP physique N° 8).
- Il y a réflexion lorsque la lumière frappe une surface lisse et qu'elle est renvoyée dans une direction déterminée.
- La réflexion peut être totale ou partielle. La réflexion est partielle si seulement une partie de la lumière est réfléchie, l'autre partie est réfractée.
2)- Première loi de DESCARTES.
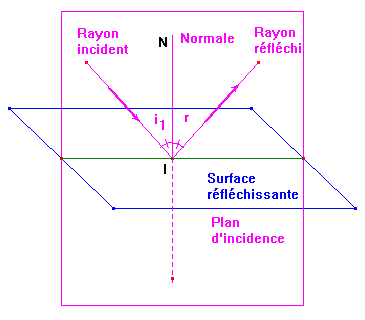
- Le rayon incident et le rayon réfléchi sont dans un même plan : le plan d'incidence.
- On appelle plan d'incidence, le plan défini par le rayon incident et la normale à la surface réfléchissante.
- Schéma :
3)- Deuxième loi de DESCARTES.
- L'angle de réflexion r est égal à l'angle d'incidence i : i = r .
- L'angle d'incidence i est l'angle formé par le rayon incident et la normale au miroir.
- L'angle de réflexion r est l'angle formé par le rayon réfléchi et la normale au miroir.
4)- Principe du retour inverse de la lumière.
- Le chemin suivi par la lumière ne dépend pas de son sens de propagation.
II- Étude expérimentale de la réfraction.
- La réfraction est le passage de la lumière d'un milieu transparent dans un autre.
- Elle provoque le plus souvent un changement de la direction de la propagation de la lumière.
2)- Première loi de DESCARTES - SNELL.
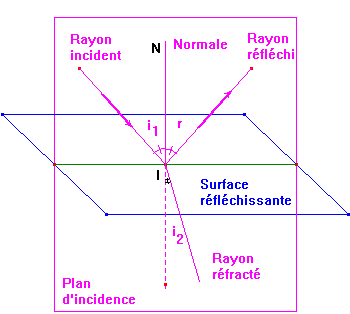
- Le rayon incident et le rayon réfracté sont dans le même plan : le plan d'incidence.
- Schéma :
3)- Deuxième loi de DESCARTES - SNELL.
- L'angle de réfraction i2 est généralement différent de l'angle d'incidence i1.
- Lorsque l'on trace sin i1 = f (sin i2) , la courbe obtenue est une droite qui passe par l'origine.
- Il découle de ceci que
![]()
- Le milieu 1 est caractérisé par l'indice de réfraction n1 et le milieu 2 est caractérisé par l'indice de réfraction n2.
- Le coefficient k représente l'indice de réfraction du milieu 1 par rapport au milieu 2 :
- Le coefficient k est égal au quotient de l'indice de réfraction du milieu 2 et de l'indice de réfraction du milieu 1.
-
![]()
- En conséquence :
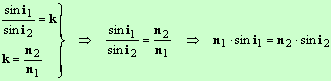
1)- Mise en évidence expérimentale.
a)- Premier cas : le rayon lumineux passe du milieu 1 l'air d'indice n1 ≈ 1 au milieu 2, le plexiglas d'indice n2 ≈ 1,5.
- En conséquence : n1 < n2
- On dit que le milieu 2 est plus réfringent que le milieu 1.
- Le rayon réfracté se rapproche de la normale au plan d'incidence.
- L'angle de réfraction est plus petit que l'angle d'incidence : i1 > i2.
- Si l'on fait varier l'angle d'incidence i1, on observe toujours un rayon réfracté.
|
Simulation à l'aide de l'animation
|
- Étude théorique :
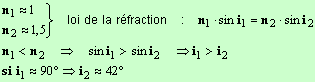
- Quelle que soit la valeur de l'angle d'incidence, il y a toujours un rayon réfracté.
b)- Deuxième cas : le rayon réfracté passe du milieu 1 le plexiglas au milieu 2 l'air.
- n1 ≈ 1,5 et n2 ≈ 1,0 en conséquence : n1 > n2
- le milieu 1 est plus réfringent que le milieu 2.
- Le rayon réfracté s'éloigne de la normale au plan d'incidence.
- L'angle de réfraction est plus grand que l'angle d'incidence : i1 < i2 .
- Si l'on augmente la valeur de l'angle d'incidence i1, on remarque que lorsque dépasse i1 une certaine valeur, on n'observe plus de rayon réfracté (ici, i1≈ 42 °).
- Cet angle est appelé : angle de réfraction limite i1≈ 42 °. Toute la lumière est réfléchie par la surface de séparation plexiglas / air. C'est le phénomène de réflexion totale.
- La réflexion totale se produit lorsque l'angle d'incidence est supérieur à une valeur limite il = λ telle que :
![]() .
.
- Étude théorique :

- Or 0 ≤ sin i2 ≤ 1 et i2 ne peut pas dépasser 90°.
Pour qu'il y ait réfraction, l'angle d'incidence i1 ne peut pas dépasser une valeur limite maximale il correspondant à i2 = 90° .

- La réflexion totale se produit lorsque le rayon lumineux arrive sur la surface de séparation des deux milieux sous un angle d'incidence supérieur à la valeur limite il .
2)- Applications de la réflexion totale.
- Fontaines lumineuses, le prisme à réflexion totale, les fibres de verre, les fibres optiques.
2)- Applications : Conseils