|
Radioactivité |
|
|
|
|
|
|
QCM N° 05
La radioactivité
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Un noyau
|
Z
protons
et A
électrons |
Z
protons
et A
nucléons |
Z
protons
et A
neutrons |
B |
|
2 |
Le noyau
d’oxygène
|
15 nucléons,
8 protons,
7 neutrons |
15 nucléons,
dont 7 protons,
et 8 neutrons |
15 nucléons,
dont 8 protons,
et 7 neutrons |
C |
|
3 |
Le symbole d’un
noyau
d’aluminium
contenant
13 protons et 14
neutrons
est : |
|
|
|
C |
|
4 |
Parmi les
affirmations
suivantes,
laquelle ou
lesquelles sont
vraies : |
Deux noyaux
sont isotopes
s’ils contiennent
des nombres
de neutrons
différents |
Deux noyaux
sont isotopes
ont le même
nombre de
protons |
Dux noyaux
ayant le même
nombre de
protons sont
isotopes l’un
de l’autre |
B |
|
5 |
Le silicium
naturel contient
14 protons et 14
neutrons
dans son noyau.
Lequel ou
lesquels des
noyaux
suivants sont
isotopes du
silicium
naturel ? |
|
|
|
BC |
|
6 |
Le fluor naturel
a pour
symbole
. Lequel
ou lesquels des
noyaux
suivants sont
isotopes
du fluor
naturel ? |
Un noyau
contenant
9 protons
et 9 neutrons |
Un noyau
contenant
10 protons
et 9 neutrons |
Un noyau
contenant
9 protons et
10 neutrons |
A |
|
7 |
La demi-vie d’un
noyau
radioactif est : |
La durée
nécessaire à
la désintégration
de la moitié
des noyaux
radioactifs d’un
échantillon. |
La moitié
de la durée
nécessaire à
la désintégration
de tous les
noyaux radioactifs
d’un échantillon |
La durée
nécessaire
pour qu’un
tel noyau
se désintègre
à moitié. |
A |
|
8 |
Soit un noyau
radioactif
de demi-vie
trente minutes.
On considère un
échantillon
contenant un
grand nombre
de ces noyaux. Au
bout
d’une heure, le
nombre de
noyaux
radioactifs
dans
l’échantillon : |
est nul |
a été divisé
par quatre |
est égal à
seulement
25 %
du nombre
initial |
BC |
|
9 |
Un échantillon de
noyaux
radioactifs
contient
initialement
N0
= 4 × 1012 noyaux d’une
même sorte. Au
bout de
quatre jours, il
en reste
N
= 1 × 1012.
La demi-vie de ce
type de
noyaux est :
|
Un
jour |
Deux
jours |
Quatre
jours |
B |
|
10 |
Soit un
échantillon de noyaux
radioactifs, dont
la demi-vie
est 1 an. Si les
trois quarts des
noyaux
initialement présents
ont disparu,
alors
l’échantillon a : |
Un an |
Deux ans |
Trois ans |
B |
|
11 |
Soit un noyau
radioactif de
demi-vie égale à
10 ans. On
considère un échantillon
contenant
initialement huit
mille milliards
de ces noyaux
radioactifs. La
courbe
représentant la
décroissance
radioactive de
cet
échantillon est :
|
|
|
|
A |
|
12 |
D’après la courbe
de
désintégration
d'un échantillon
de noyaux de
plomb 201,
la demi-vie du
plomb est
voisine de :
|
100 ans |
40 ans |
20 ans |
C |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Symbole du noyau d’un atome :
-
Le noyau, d’un atome ou d’un ion de
symbole chimique X,
-
Comporte :
Z protons et
A nucléons (et
A –
Z neutrons).
-
On le note :
![]() .
.
-
Nombre de masse :
A
-
Nombre de charge :
Z
Noyau de l’atome d’oxygène :![]()
-
Noyau d’oxygène :
-
Z
= 8 : il possède 8 protons
-
A
= 15 : nombre de nucléons : 15
-
Dont : 8 protons et A – Z
= 7 neutrons.
Le symbole d’un noyau d’aluminium :
-
Z
= 13 : il possède 13 protons
-
A – Z
= 14 neutrons
-
A = Z
+ 14 = 13 + 14 = 27
-
![]()
Isotopes :
-
Des atomes ou des ions
isotopes possèdent le même nombre de protons Z
et un nombre de neutrons N
différent.
-
Ils ont le même numéro
atomique Z, mais un nombre de
nucléons A différent
-
(A
= Z +
N)
-
Les atomes isotopes
portent le même nom que l’élément chimique auquel ils appartiennent, suivi de
leur nombre de nucléons A.
-
Exemple :
|
Atomes isotopes |
|||||||
|
12
6 |
C |
|
13
6 |
C |
|
14
6 |
C |
|
98,9 % |
1,1 % |
Traces |
|||||
|
Composition d'un morceau de graphite |
|||||||
Le silicium :
-
Noyau de silicium :
Z = 14
-
A
= 27 pour l’isotope Si 27 et
A = 29 pour
Si 29
-
Si
27 ( protons 14 et neutrons 13) et
Si
29 (protons 14 et neutrons 15)
Le fluor :
-
![]() et l’isotope
et l’isotope
![]()
Demi-vie :
-
Pour un type de noyaux
radioactifs, la demi-vie t1/2
est la durée au bout de laquelle la moitié des noyaux radioactifs initialement
présent dans l’échantillon se sont désintégrés.
-
Relation entre
t1/2
et λ :
-
Au temps
t : N (t) = N
0 e
– λ . t
-
Au temps
t + t
1/2 :
-
N (t + t1/2
) = N0
e – λ . (t + t1/2)
-
![]()
-
En conséquence :
-
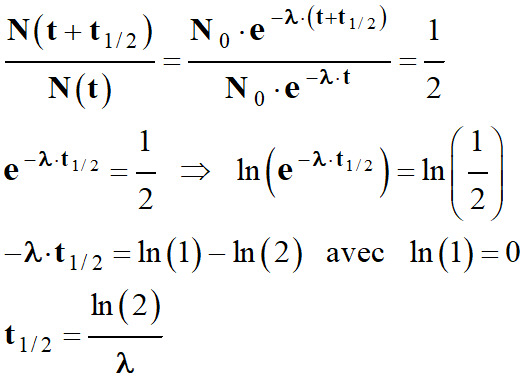
-
La demi-vie n’a qu’une valeur
statistique.
-
Elle indique qu’un noyau radioactif a
une chance sur deux de disparaître au bout d’une demi-vie.
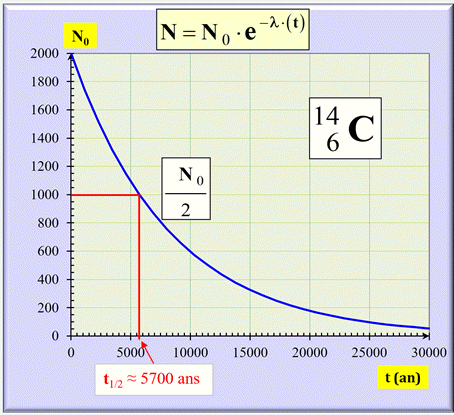
-
Évolution en fonction de la demi-vie :
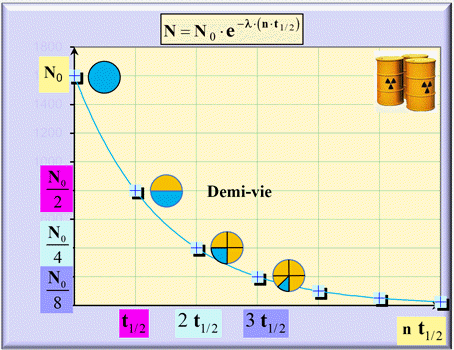
-
On considère que 99 % d’une population
de noyaux radioactifs est désintégrée après une durée de sept demi-vies environ.
-
Au bout de
1
t½ => N
= N0
/ 21 :
-
Au bout de
2
t½ => N
= N0
/ 22 :
-
Au bout de
3
t½ => N
= N0
/ 23.
Noyau radioactif et demi-vie :
-
Au bout de
1
t½ => N
= N0
/ 21 :
-
Au bout de
2
t½ => N
= N0
/ 22 :
-
Au bout de
3
t½ => N
= N0
/ 23.
-
Si on considère qu’au temps
t, il y a 100
noyaux radioactif :
-
Au bout de 30 min, il en reste 100 / 2
= 50
-
et au bout d’une heure 50 / 2 = 25
-
il en reste 25 %
Demi-vie et noyau radioactif :
-
Au bout de
1
t½ => N
= N0
/ 21 :
-
Au bout de
2
t½ => N
= N0
/ 22 :
-
Au bout de
3
t½ => N
= N0
/ 23.
-
Dans le cas présent :
-
N =
N0
/ 4, ceci au bout de 4 jours
-
t ½ =
2 jours
Noyaux radioactifs et demi-vie :
-
Au bout de
1
t½ => N
= N0
/ 21 :
-
Au bout de
2
t½ => N
= N0
/ 22 :
-
Au bout de
3
t½ => N
= N0
/ 23.
-
Il reste 25 % des noyaux radioactifs.
-
Le nombre de noyaux radioactifs a été
divisé par 4.
-
L’échantillon a deux ans.
Courbe de décroissance radioactive :
-
Au départ
N0
= 4 × 1012 noyaux
-
Au bout de 10 ans :
N =
N0
/ 2 = 2 × 1012 noyaux
-
Au bout de 20 ans :
N =
N0
/ 4 = 1 × 1012 noyaux

Courbe de décroissance radioactive : Exploitation :

|
|