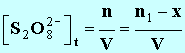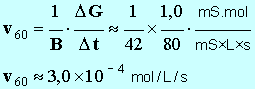|
Exercice 3 : 6 pts |
Bac Blanc Décembre 2004 : |
|
|
|
Exercice
3 : Étude cinétique par conductimétrie (6 points)
|
Dans cet exercice, on s'intéresse à la réaction d'oxydoréduction entre les ions peroxodisulfate
S2O82
– Dans un bécher, on introduit un volume V1 = 40 mL d'une solution aqueuse de
peroxodisulfate de potassium ( 2
K
+ (aq)+
S2O82
– C1 = 1,0 x 10 – 1 mol / L . à l'instant t = 0 s, on ajoute un volume V2 = 60 mL d'une solution aqueuse
d'iodure de potassium (
K +
(aq)+
I
– Un conductimètre, relié à un système d'acquisition de données, permet de suivre l'évolution de la conductance de la solution au cours du temps. La courbe obtenue est reproduite ci-dessous.
1. L’équation de cette réaction d’oxydoréduction entre les ions peroxodisulfate S2O8 2 – et les ions iodure I – en solution aqueuse s’écrit : S2O8 2 – (aq) + 2 I – (aq) = 2 SO4 2 – (aq) + I2 (aq) - Écrire les demi-équations électroniques pour chacun des deux couples qui interviennent dans cette réaction et donner les couples oxydant / réducteur. 2. Déterminer le réactif limitant. En déduire la valeur de l'avancement maximal xmax de la réaction. 3. En notant x l'avancement de la réaction à l'instant t, donner les expressions des concentrations des divers ions présents dans le mélange en fonction de x et ou du volume V de la solution. On négligera les ions H3O+et HO – très minoritaire devant les autres ions. 4. Donner la relation liant la conductance G d'une telle solution, les caractéristiques de la cellule, les conductivités molaires ioniques et les concentrations des ions qu'elle contient à l’instant t.
5. En simplifiant, on peut montrer que la relation entre la conductance
G et
l’avancement
x de la réaction est de la forme :
où V est levolume total de la solution, constant pendant toute la durée de l'expérience. Pour la suite de l'étude, on donne les valeurs des constantes (dans les conditions de l'expérience) : A = 1,9 mS . L et B = 42 mS . L . mol – 1 . Définir la vitesse volumique de la réaction en fonction de l'avancement x. En déduire son expression en fonction de G. 7. En utilisant la courbe G = f (t), déterminer avec un seul chiffre significatif la valeur de l'avancement final de la réaction. 8. Donner la définition du temps de demi-réaction, puis déterminer graphiquement sa valeur. 9. Calculer la valeur du taux d'avancement de la réaction. Conclure. |
|
Dans cet exercice, on s'intéresse à la réaction d'oxydoréduction entre les ions peroxodisulfate
S2O82
– Dans un bécher, on introduit un volume V1 = 40 mL d'une solution aqueuse de
peroxodisulfate de potassium ( 2
K
+ (aq)+
S2O82
– C1 = 1,0 x 10 – 1 mol / L . à l'instant t = 0 s, on ajoute un volume V2 = 60 mL d'une solution aqueuse
d'iodure de potassium (
K +
(aq)+
I
– Un conductimètre, relié à un système d'acquisition de données, permet de suivre l'évolution de la conductance de la solution au cours du temps. La courbe obtenue est reproduite ci-dessous.
1. L’équation de cette réaction d’oxydoréduction entre les ions peroxodisulfate S2O8 2 – et les ions iodure I – en solution aqueuse s’écrit : S2O8 2 – (aq) + 2 I – (aq) = 2 SO4 2 – (aq) + I2 (aq) - Écrire les demi-équations électroniques pour chacun des deux couples qui interviennent dans cette réaction et donner les couples oxydant / réducteur. - Demi équations électroniques :
- Couples oxydant / réducteur : I2 (aq) / I – (aq) et S2O8 2 – (aq) / SO4 2 – (aq) 2. Déterminer le réactif limitant. En déduire la valeur de l'avancement maximal xmax de la réaction. - Tableau d’avancement :
- Quantités de matières des réactifs à l’instant initial :
- Quantité de matière d’ions peroxodisulfate :
- n1 = C1 . V1 ≈ 1,0 x 10 – 1 x 40 x 10 – 3 mol - n1 ≈ 4,0 mmol - Quantité de matière de diiode : - n2 = C2 . V2 ≈ 1,5 x 10 – 1 x 60 x 10 – 3 mol - n2 ≈ 9,0 mmol
- Il faut résoudre
le système d’inéquations suivant : :
3. En notant x l'avancement de la réaction à l'instant t, donner les expressions des concentrations des divers ions présents dans le mélange en fonction de x et ou du volume V de la solution. On négligera les ions H3O+et HO – très minoritaire devant les autres ions. - Expressions des concentrations des divers ions présents : - - - - Remarque : cette expression n'est pas
demandée ( pas ion) :
4. Donner la relation liant la conductance G d'une telle solution, les caractéristiques de la cellule, les conductivités molaires ioniques et les concentrations des ions qu'elle contient à l’instant t. - Conductance de la solution :
5. En simplifiant, on peut montrer que la relation entre la conductance
G et
l’avancement
x de la réaction est de la forme :
où V est levolume total de la solution, constant pendant toute la durée de l'expérience. Pour la suite de l'étude, on donne les valeurs des constantes (dans les conditions de l'expérience) : A = 1,9 mS . L et B = 42 mS . L . mol – 1 . Définir la vitesse volumique de la réaction en fonction de l'avancement x. En déduire son expression en fonction de G.
- Pour déterminer la valeur de la vitesse, on trace la tangente à la courbe au point considéré, on détermine la valeur du coefficient directeur de cette tangente et on divise le résultat obtenu par B. -
Cliquer sur l'image pour l'agrandir -
Cliquer sur l'image pour l'agrandir 7. En utilisant la courbe G = f (t), déterminer avec un seul chiffre significatif la valeur de l'avancement final de la réaction. - Avancement final : - Lorsque la réaction est terminée,
G ≈
20,65 mS. - À partir de la relation suivante : -
- avec 1 seul chiffre significatif : x f ≈ 4 mmol 8. Donner la définition du temps de demi-réaction, puis déterminer graphiquement sa valeur. - Temps de demi-réaction : durée au bout de laquelle l’avancement de la réaction est égal à la moitié de l’avancement final. - - Valeur de la conductance de la solution à t ½ : - - La lecture graphique donne : t ½ ≈ 35 s. 9. Calculer la valeur du taux d'avancement de la réaction. Conclure. - Valeur du taux d’avancement de la réaction :
- La réaction est quasi totale. On peut écrire : S2O8 2 –(aq) + 2 I – (aq) → 2 SO4 2 – (aq) + I2 (aq) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||