Objectif : Savoir positionner des objets les uns par rapport aux autres sur une échelle des distances.

 Matériel : film ou CD-ROM les puissances de dix, ordinateur.  

I- Les puissances de 10.

1)- Rappels.

-  Longueur, masse, intensité du courant, …sont des grandeurs physiques.

-  Le résultat de la mesure d’une grandeur physique s’exprime par un nombre toujours suivi d’une unité.

- Exemples :

-  Unité de longueur le mètre (m), unité de masse le kilogramme (kg), unité d’intensité du courant, l’ampère (A).

- Exemples : 1000 = 1 x 10 ³  et  0,001 = 1 x 10 ^{- 3}

Compléter le tableau des opérations avec les puissances de 10 (document 1).

2)- L’écriture scientifique.

Sans calculatrice et en s’aidant du document 1, donner l’écriture scientifique du nombre A, sachant que :

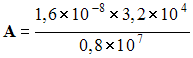
Vérifier le résultat avec la calculatrice.

 3)- Multiples et sous-multiples.

- Pour évaluer, appréhender certains résultats numériques,

il est parfois utile de les exprimer à l’aide d’un multiple ou d’un sous-multiple de l’unité.

- Exemple :

-  le kilomètre est un multiple du mètre.

-  On dit que la distance Manosque – Aix est d’environ 55 km plutôt que 5,5 × 10 ⁴ m.

Compléter le tableau (document 2).

II- Analyse d’un document vidéo.

1)- Visualisation du document vidéo.

Le film les puissances de 10 permet de voyager de l’infiniment petit vers l’infiniment grand.

-  Lors de sa projection, compléter le tableau (document 3).

2)- Exploitation du document 3.

- Il s’agit de compléter à nouveau le tableau avec d’autres objets dont les dimensions sont les suivantes :

- Distance de l’étoile la plus proche du Soleil : 4,2 a.l. :  

- Distance Terre – Soleil : 150 millions de kilomètres :  

- Diamètre d’un pamplemousse : 10 cm :  

Convertir ces trois distances en mètre sachant que 1a.l. = 9,5 × 10¹⁵ m et donner chaque résultat sous forme d’une puissance de dix.

Donner un ordre de grandeur pour ces trois distances :

- Écrire la valeur considérée en écriture scientifique,

- Chercher la puissance de 10 la plus proche de la valeur ainsi écrite,

- On utilisera la règle suivante :

- Si le nombre est inférieur à 5, l’ordre de grandeur est égal à la puissance de dix

- Si le nombre est supérieur ou égal à 5, l’ordre de grandeur est égal à 10 multiplié par la puissance de dix.

- Présenter les résultats sous forme de tableau :

- Exemples :

- 2,72 × 10 ⁴ a pour ordre de grandeur :  10⁴

- 8,7 × 10 ⁴ a pour ordre de grandeur :  10⁵  

Insérer à leur place, dans le tableau (document 3) ces nouvelles valeurs.

III- Taille comparée des différents systèmes.

1)- Construction d’une échelle particulière.

- On compare les tailles des différents systèmes qui constituent l’Univers grâce à une échelle particulière.

Préparation de la graduation.

- Prendre une feuille de papier (21 cm x 29,7 cm) à petits carreaux.

- Tracer au centre de la feuille un axe orienté de gauche à droite. À l’extrême droite, placer la graduation 10 ²⁵.

- Placer les autres graduations régulièrement espacées de 0,5 cm (jusqu’à 10 ^{– 18} ).

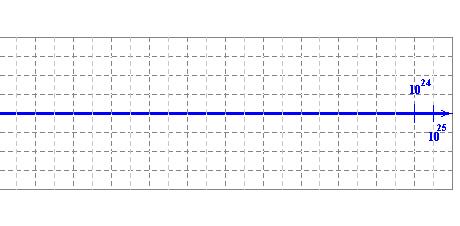
- Une puissance de dix est représentée par une graduation.

- Numéroter, en bleu, les graduations 10 ¹, 10 ²,  10 ³, 10 ⁴, …

- Pour plus de lisibilité, on peut mettre les graduations paires au-dessus de l'axe et les graduations impaires au-dessous.

- Indiquer,  en rouge, la position des multiples et des sous-multiples du mètre.

- Remarque : un tel axe ne comporte pas de zéro, ni de grandeurs négatives.

-  Sur un tel axe se côtoient, à quelques distances d’écart des nombres infiniment petits (10 ^{– 15} ) et des nombres infiniment grands (10 ¹⁵ ).

- Données : Sur l’axe ainsi gradué, placer les ordres de grandeur des données rencontrées au cours du TP. Montrer que cette échelle n’est pas linéaire.

2)- Application.

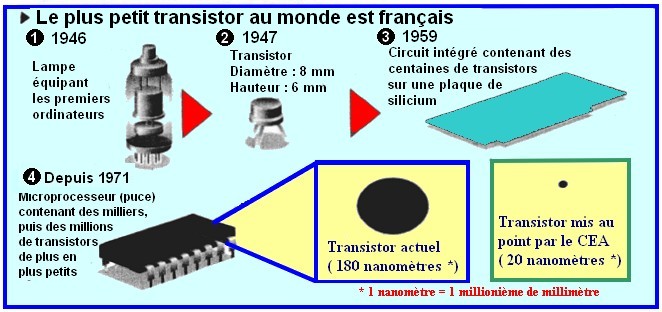
- Le texte, du document 4, est paru dans le quotidien Ouest-France le 25 septembre 1999.