TP Chimie N° 06  Concentration et conductimétrie, correction, Première S

TP Chimie. N° 06

Concentration et conductimétrie.

Correction

Enoncé

   



 

But : détermination de la concentration d’un sérum physiologique

 

I - Protocole expérimental.

1)- Montage.

2)- Etalonnage du conductimètre.

II - Les mesures.

1)- Mode opératoire.

2)- Préparation du sérum pour la mesure.

III - Exploitation des résultats.

IV - Application.

 

Matériel :

- Un G.B.F, deux multimètres (un noir et un jaune), une cellule de conductimétrie,

- Des fils de connexion,

- Des fioles jaugées de 100 mL, des pipettes graduées ou des pipettes jaugées (à voir),

- Un flacon de sérum physiologique, de l’eau distillée,

- Une solution de chlorure de sodium de concentration :

-  C0 = 1,0 mmol / L. C1 = 2 mmol / L, C2 = 3 mmol / L, C3 = 4 mmol / L,

-  C4 = 5 mmol / L, C5 = 6 mmol / L, C6 = 7 mmol / L, C7 = 8 mmol / L,

-  C8 = 9 mmol / L, C9 = 10 mmol / L, C10 = 12 mmol / L, C11 = 14 mmol / L

 

 Objectifs :

-   Tracer une courbe d’étalonnage.

-   Le sérum physiologique est une solution aqueuse de chlorure de sodium.

-   Le but de cette manipulation est de déterminer la concentration molaire de ce sérum en utilisant la conductimétrie.

 

I- Protocole expérimental.

1)- Montage.

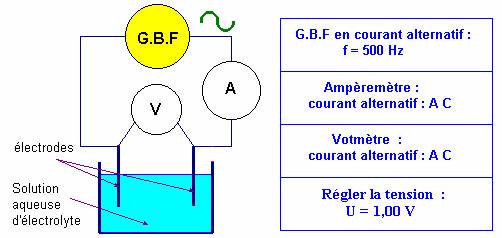
-   Schéma et montage :

 

Attention à la position des sélecteurs avant d'effectuer les mesures.

-   Schématiser et effectuer le montage du conductimètre.

2)- Étalonnage du conductimètre.

ManipulationPlonger la cellule dans un bécher contenant de l’eau distillée.

-   Réglage du G.B.F : régler la fréquence sur 500 Hz et la valeur de la tension sur  U = 1,0 V 

(Cette valeur doit être maintenue constante au cours de l’expérience).

-   Mesurer la valeur de l’intensité Ib.

-   Ceci constitue le « blanc ».

-   On quantifie ici la présence d’éventuelles impuretés dans l’eau. 

-   La valeur mesurée devra être systématiquement soustraite des autres valeurs mesurées pour éliminer la contribution de ces impuretés.

II- Les mesures.

1)- Mode opératoire.

ManipulationPlonger successivement la cellule dans les douze solutions d’étalonnage.

-   Pour chaque mesure, vérifier la valeur de la tension (U = 1,0 V) avant de relever la valeur de l’intensité I.

-   Penser à rincer la cellule après chaque mesure puis à éliminer la majeure partie de l’eau de rinçage (papier joseph) sans perturber la cellule.

-   Au début de la mesure suivante, agiter doucement la cellule pour bien homogénéiser.

cellule conductimétrique

Animation CabriJava pour effectuer les mesures

RédactionReproduire et compléter le tableau suivant :

C   

(mmol / L)

0,0

1,0

2,0

3,0

4,0

5,0

6,0

7,0

8,0

9,0

10,0

12,0

14,0

I   

(mA)

 

 

 

 

 

 

 

 

 

 

 

 

 

G

(mS)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-   On effectue le blanc avec la solution d’eau distillée :

U

1,008 V 

I b =

0,04  mA

-   Tableau de valeurs : Valeur de la tension : U = 1,008 V

 

C  

 (mmol / L)

0,0

1,0

2,0

3,0

4,0

5,0

6,0

7,0

8,0

9,0

10,0

12,0

14,0

I   (mA)

0,01

0,87

1,16

1,61

2,13

2,64

3,31

3,65

4,18

4,63

5,16

6,04

7,08

G = I / U

(mS)

0,01

0,86

1,15

1,60

2,11

2,62

3,28

3,62

4,15

4,59

5,12

5,99

7,02

G corrigé

(mS)

0,00

0,82

1,11

1,56

2,07

2,58

3,24

3,58

4,11

4,55

5,08

5,95

6,98

2)- Préparation du sérum pour la mesure.

a)- concentration massique de la solution de sérum physiologique : 

-   Relever l’indication que porte le flacon de sérum physiologique acheté en pharmacie.

-  Titre massique de la solution de sérum physiologique : t = 9,0 g / L.

RédactionEn déduire la valeur de la concentration molaire CS.

-  Concentration molaire C S :

-  M ≈ M  (Na) + M (Cl)  =>  M ≈ 23,0  +  35,5  =>    M ≈ 58,5 g / mol

-   

b)-      Dilution.

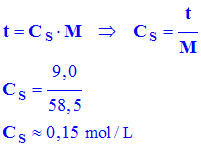
ManipulationCette solution étant trop concentrée, il faut la diluer 20 fois (9,0 g / L) ou 100 fois. 

-   Proposer un mode opératoire permettant de préparer 100 mL de solution diluée.

-   La préparer et effectuer la mesure.

-   Dilution : Comme on utilise la solution commerciale à 9,0 g / L, il faut diluer 20 fois :

 

S

{

C S = 0,15 mol / L

Dilution

S F

{

C F = C S / 20

V S = ?

→

V F = 100 mL

n S  = C S . V S

 

n F  = C F . V F

Solution mère

 

Solution fille

 

-   Volume de solution commerciale nécessaire :

-   Au cours de la dilution, il y a conservation de la quantité de matière de soluté :

-   nS  = nF   =>  CS . VS  = CF . VF

-   VS  = VF / 20

-   VS  = 10  mL

-   Mode opératoire :

Première étape :

Verser suffisamment

de solution Mère

dans un bécher

Deuxième étape :

On prélève le

volume nécessaire 

de solution Mère

à l’aide d’une

 pipette jaugée munie

de sa propipette

Troisième étape :

On verse le

volume nécessaire

de solution dans

la fiole jaugée de

 volume approprié..

On ne pipette jamais

directement dans

le flacon qui contient

la solution Mère

Quatrième étape :

On ajoute de l’eau

distillée et on agite

 mélanger et

 homogénéiser

Cinquième étape :

On complète avec

une pissette

 d’eau distillée

jusqu’au trait

de jauge.

Sixième étape :

on agite pour

homogénéiser. 

La solution

est prête.

 

-   Concentration de la solution fille : CF = CS / 20 ≈ 7,5 x 10 – 3 mol / L  

III- Exploitation des résultats.

RédactionTracer la courbe d’étalonnage représentative de la variation de la conductance G en fonction de la concentration C : G = f (C).

-   Donner les caractéristiques de la courbe obtenue. Quelle allure aurait cette courbe si on ne tenait pas compte du « blanc » ?

-   Les points sont sensiblement alignés. On peut tracer la droite moyenne. 

-   Avec Excel, on ajoute une courbe de tendance et comme modèle ‘’linéaire’’

-   La courbe obtenue est une droite qui passe pratiquement par l’origine. 

-   On peut affirmer que la conductance de la solution est proportionnelle à la concentration de la solution, ceci dans le domaine étudié.

-   On tire : G (mS) ≈ 0,489 C (mmol / L)

-   Si on ne tient pas compte du « blanc » : 

-   Dans le cas présent, l’écart entre les deux courbes est minime car l’eau ''distillée'' utilisée est peu conductrice.

-   Quelle relation simple existe-t-il entre la concentration et la conductance lorsque l’électrolyte est suffisamment dilué ?

-   Donner cette relation.

-   On tire : G (mS) ≈ 0,489 C (mmol / L)

-  (Le coefficient de détermination est proche de 1 : R2 ≈ 0,9982 )

-   Que se passe-t-il lorsque l’électrolyte est trop concentré ?

-   Lorsque l’électrolyte est trop concentré, il n’y a plus proportionnalité entre la conductance et la concentration de la solution.

-   À l’aide de la courbe, déduire la concentration molaire en chlorure de sodium de la solution diluée de sérum physiologique.

-   Concentration molaire correspondante à la solution commerciale :

-   Exploitation graphique :

 

Mesure

Sérum physiologique

Solution diluée

I = 3,8 mA

U = 1,008 V

I b = 0,040 mA

Conductance

G  = 3,76 mS

-   En déduire la concentration molaire correspondante à la solution commerciale. La comparer à la valeur CS. Conclusion.

-   Concentration de la solution commerciale diluée : C ≈ 7,3 mmol / L

-   Concentration de la solution commerciale : CS = 20 C ≈ 7,3 mmol / L

-   CS ≈ 0,14 mol / L

-   Calcule d’erreur :  

-   

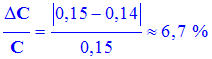
-   Le résultat est médiocre !!!

IV- Application.  

Détermination de la concentration d’une solution

L’hypocalcémie, carence de l’organisme en élément calcium,

peut être traitée par injection intraveineuse  d’une solution de chlorure de calcium

(Ca2+ (aq)  +  2 Cl- (aq)). 

Pour déterminer sa concentration C, on utilise une méthode conductimétrique.

1. On dispose, pour étalonner la cellule conductimétrique, de solutions étalons Si de concentrations connues Ci.

-   Le tableau suivant fournit les conductances Gi de ces différentes solutions.

Solution Si

S1

S2

S3

S4

S5

C i (mmol / L)

10,0

7,5

5,0

2,5

1,0

G i (mS)

5,88

4,45

2,97

1,49

0,6

-   Tracer la courbe G = f (C).

2.  Le contenu d’une ampoule de solution injectable a été dilué 100 fois.

La mesure de la conductance de la solution diluée, avec la même cellule conductimétrique et à la même température, donne :

G’ = 2,71 mS.

a. Déterminer la valeur de la concentration C’ de la solution diluée.

b. En déduire la concentration C de la solution injectable.

c. Pourquoi a-t-il été nécessaire de diluer cette solution ?

3. Déterminer l’apport calcique, c’est-à-dire la quantité d’élément calcium, d’une ampoule de solution injectable de 10,0 mL.

 

 

Correction :

 

Détermination de la concentration d’une solution

1. Courbe G = f (C).

-   Les points sont sensiblement alignés.

-   On peut tracer la droite moyenne. 

-   Avec Excel, on ajoute une courbe de tendance et comme modèle ‘’linéaire’’

-  La courbe obtenue est une droite qui passe pratiquement par l’origine. 

-  On peut affirmer que la conductance de la solution est proportionnelle

à la concentration de la solution, ceci dans le domaine étudié.

-  On tire : G (mS) ≈ 0,588 C (mmol / L)

2. Conductance de la solution diluée

a. Concentration C’ de la solution diluée.

-  Exploitation graphique : C’ ≈ 4,6  mmol / L ≈ 4,6 x 10– 3 mol / L

b. Concentration C de la solution injectable.

-   C = 100 C’  =>  C = 100 x 4,6 x 10– 3  =>  C ≈ 4,6 x 10– 1  mol / L

c. Pourquoi a-t-il été nécessaire de diluer cette solution ?

-  La concentration de la solution injectable est supérieure à la concentration de la solution S0.

-  Elle n’appartient pas au domaine d’étude.

-  La loi n’est plus vérifiée pour les solutions trop concentrées.

3. Apport calcique d’une ampoule de solution injectable de 10,0 mL.

-  Par définition : n (Ca 2+) = [Ca 2+] . V

-  n (Ca 2+) = 4,6 x 10– 1 x 10,0 x 10– 3

-  n (Ca 2+) ≈ 4,6 x 10– 3 mol